A Radical Approach to Lebesgue’s Theory of Integration : Summary

This book is the sequel to the book A Radical Approach to Real Analysis, a book that I found to be the best historical narrative of Real Analysis. This book too in the same league, though applied to Lebesgue theory. Let me attempt to summarize this fascinating book. The book comprises 8 chapters structured in such a way that it takes the reader from Riemann integral to Lebesgue integral and finally answering  a simple but revolutionary question in analysis, “ When does a function have a Fourier Series expansion that converges to that function? ”

**Chapter 1 : Introduction
**The first chapter starts off with emphasizing the five big questions that occupied the centre stage in the 19th century

1. When does a function have a Fourier series expansion that converges to that function?

2. What is integration?

3. What is the relationship between integration and differentiation?

4. What is the relationship between continuity and differentiability?

5. When can an infinite series be integrated by integrating each term?

One can say that the first chapter kind of summarizes quickly Volume I from the same author, titled “A Radical approach to Real Analysis”. Let me attempt to summarize the summary –:) . Basically the first enlightening counter example in real analysis was Dirchlet’s function which questioned the notion that function was some geometric concept, representable only as curves. Newton and Leibniz while grappling with physics problems came out with integration as a tool to help them in their quest. Most of the definitions were based on infinitesimals, which were looked upon by others with a skeptic eye. According to George Berkley, they were “ghosts of departed quantities”. In such an environment, Cauchy’s integral definition based on approximating finite sums was very elegant mathematically.

Riemann came along and then modified Cauchy’s approximating finite sums definition which proved a better way of integrating. Why is Riemann method superior to Cauchy’s? The author promises to answer this question at a later point in the book. Thanks to Fundamental theorem of Calculus, definite integral was viewed from the lens of anti-derivative function. Of course not all functions have anti derivatives that can be expressed in terms of standard functions. One can safely say that counterexamples paved the way for greater understanding in real analysis than any other field. Darboux example of continuous functions, not differentiable anywhere , challenged the prevalent view that “continuous functions would have to be differentiable at most points “ Weierstrass developed and worked on the concept of uniform convergence to bring sanity in to situations where term by term integration could be applied. Unfortunately , uniform convergence proved to be a sufficient condition than a necessary condition for term-by-term integration. Fourier series is a classic example where the series is not uniformly convergent but term-by-term integration makes sense. By the end of the introductory chapter, one realizes that clinging to Riemann definition would only cloud the linkages between continuity-differentiability-integrability-term by term integration issues.

Chapter 2 : The Riemann Integral
The second chapter talks about Riemann integrability. Riemann improved upon Cauchy and made it more generic by considering the value of the function at an arbitrary point in a partition. He then used Cauchy criterion for convergence to compute the integral value. Gaston Darboux digged in to the Riemann’s paper on definite integral and came up with conditions for Riemann integrability for any bounded closed function. Even though Riemann presented his workings, he was concerned about the linkage between continuity and differentiability. He presented a pathological function which was discontinuous at every rational number with an even denominator but was still integrable. This was followed up by a few more counter examples which showed that there existed functions which were everywhere continuous but nowhere differentiable functions. There were still many open questions that had to be worked on. The representation of Fourier series ranked high in the priority list of open problems. Given that a function can be represented as a sum of infinite trigonometrical series, Riemann turned the situation around and thought about the following questions:

• Does a trigonometric series have to be integrable?

• Is the Fourier series always identical to the series which we started?

• Some of the interesting Fourier series converged to discontinuous functions and thus were not uniformly convergent. So, what can one say about functions which are not uniformly convergent ?

In this context, the chapter talks about three mathematicians whose work paved way to greater understanding. First was Eduard Heine. Heine was the first mathematician to describe a way out by coming up with “ Uniform convergence in general”, which he defined as a series with finitely many exceptional points that is uniformly convergence on any closed interval that does not contain one of these points. He thus went on to prove that a set of trigonometric functions which are uniformly convergent in general , no two distinct series converges to the same function.

Second mathematician mentioned is Hermann Hankel who grappled with the discontinuous functions and tried classifying them in to groups based on how Riemann integrable they are. He came up with a concept of set being dense and categorized discontinuous functions. His final conclusion was that a function that is point-wise discontinuous must be Riemann integrable. However this was a faulty conclusion, thanks to the counter example by H.J.S Smith. Georg Cantor is mentioned as the trio from the “Class of 1870” who realized that there is something far more important that had to be worked on, before talking about Riemann Integrability, continuity and differentiability – The Real Line.

**Chapter 3 : Explorations of R
**The third chapter is a brief summary of topology in relation to the metric space R. Basic definitions of neighbourhood, open sets, closed sets, compact sets, interior points, closure points, boundary points, dense set are given. The chapter then goes on to discuss means to accommodate algebra on Real line. A word based proof is given for Bolzano-Weierstrass theorem which is by far the best way to present the proof that I have come across. Concept of completeness is introduced subsequently where any ONE of the properties is equivalent to the other three, the properties/theorems being,

• Every sequence of closed, nested intervals has a nonempty intersection that belongs to the set

• Every bounded subset has a least upper bound in the set

• Every Cauchy sequence converges to a point in the set

• Every infinite bounded subset has a limit point in the set

The highlight of this chapter is to discuss the drama behind Heine-Borel theorem. The story starts off with Axel Harnack who carried a mistaken notion that the complement of a countable union of intervals is also a countable union of intervals. There was a major flaw in the statement which was finally resolved by Emily Borel. Borel proved that if the sum of the lengths of the open intervals is strictly less than 1, there must be points – infact , uncountably many points – that are not in any of these intervals. Lebesgue generalized Borel’s theorem. However the name that got stuck on this property( Any open cover on a closed and bounded set has a finite subcover ) is Heine-Borel Theorem.

The story then shifts to Dirichlet who was the first to discriminate between continuity and uniform continuity. However it was later published by Heine who never gave credit to Dirichlet. The proof used by Heine was very similar to Borel and Lebesgue’s proof. Another twist to the story is that, Arthur Schönflies, 1900, who claimed Borel’s result also holds for uncountable covers, pointed out connection to Heine’s proof of uniform continuity. He was the first to call it Heine–Borel theorem and the name was further popularized by Henry Young in his paper, “Overlapping intervals”. Heine-Borel theorem subsequently appeared in many formats such as Weierstrass theorem. One historian actually refers to it as “ Dirichlet-Heine-Weierstrass-Borel-Scoenflies-Lebesgue theorem”. Borel called this theorem as “the first fundamental theorem of measure theory“, even though the name never caught on. The chapter then gives a quick Cantorian Set theory where concepts such as Cardinality, Continuum Hypothesis , Power Sets are explained

Overall, a fair treatment to the topology of R is presented in this chapter.

**Chapter 4 : Nowhere Dense Sets and the Problem with the Fundamental Theorem of Calculus
**The chapter talks about SVC sets in the context of Smith-Volterra-Cantor contribution to calculus. It starts off with the construction of cantor set and gives a description of Devils’s staircase function, a function which has infinite steps between any two steps, derivative exists and is 0 at every point in [0,1] except at values in the cantor dust. Cantor set is uncountable and hence this function is such a strange function where F’(x) = f(x) and yet the evaluation part of FTC( Fundamental Theorem of Calculus) does not hold good.

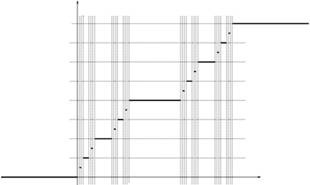
Devil’s Staircase function

Volterra’s function is an example of a function which is pointwise discontinuous and not Riemann integrable. There is also a mention of the extent to which one can come up with pathological functions which Volterra proved. He conclusively proved that inverse of Ruler function cannot exist, a function which is continuous at rationals and discontinuous at irrationals cannot exist.

Developments from Baire are mentioned as they became the precursor to Lebesgue theory. Lebesgue had to say this

“ Baire showed us how to investigate matters; which problems to pose, which notions to introduce. He taught us to consider the world of functions and to discern there the true analogies, the genuine differences. In absorbing the observations that Baire made, one becomes a keen observer, learning to analyze common place ideas and to reduce them to notions more hidden, more subtle but also more effective. ”

So, what were Baire’s contributions ?

He introduced the concept of nowhere dense sets and categorized sets in to those that can be formed as a countable union of nowhere dense sets and those that can’t be. His genius lies in acknowledging that the first category sets are sparse in nature. He is famously known for his category theorem that an open interval cannot be expressed as the countable union of nowhere dense sets. Baire was trying to improvise on Hankel’s classification. Baire’s classification went like this: Continuous functions constitute class 0. Pointwise discontinuous functions that are not continuous constitute class 1. Inductively , if f is the limit of functions in class n , but it is not in any class k<=n, then we can say that f is in class n + 1. One outcome of such a classification is that , even though point wise discontinuous functions can have infinite discontinuities, there is enough continuity on a dense set of points. What was particularly not evident in Baire’s classification was : If you define an inductive based argument for classifying functions, is there a case when a function escapes all these classes?

**Chapter 5: The Development of Measure Theory
**The chapter starts off with listing the difficulties of Riemann Integral despite of the developments in 1880’s and 1890’s such as

• It is defined for only bounded functions. While improper integrals had been introduced to deal with unbounded functions, this fix appears to be adhoc.

• It is possible to have an integrable function with positive oscillation on a dense set of points and therefore the integral is not differentiable at any of the points in the dense set. This violates the anti-differentiation part of the fundamental theorem of calculus

• It is possible to have a bounded derivative that cannot be integrated. This violates the evaluation part of the fundamental theorem of calculus

• The limit of a bounded sequence of integrable functions is not necessarily Riemann integrable( Baire’s sequence)

• The question of finding necessary and sufficient conditions under which term-by-term integration is valid was turning out to be extremely difficult

Despite these shortcomings, mathematicians did not part with Riemann integral but tried fixing the problem with improvements. Weierstrass came up with a modified version of Riemann integral but lost its steam very soon as it failed the additive property.

The chapter then introduces Giuseppe Peano, Camille Jordan and Emile Borel who formulated various concepts in set theory. Peano came up with the definition of content and showed that a set has content if its inner content was equal to the outer content. Jordan defined Jordan Measure of a set as its content and extended to finite set of disjoint measurable sets. Thus he was talking about finite additivity of content and increasing the concept to more sets. However using this concept of inner content and outercontent had one flaw. For far too many important sets , inner content was not equal to outer content. Emile Borel realized that the problem with Jordan measure was that it finitely additive. So , he introduced a new measure with countably additive property with three additional assumptions’

• The measure of a bounded interval is the length

• The measure of a countable union of pairwise disjoint measurable sets is the sum of their measures

• If R and S are measurable sets with R being a subset of S , then m(S-R) =m(S) – m(R)

However there was a limitation to Borel Measure. It was applicable to a much smaller collection of sets than Jordan measure. The cardinality of Borel measurable sets was much smaller than that of Jordan measurable sets

The concept of countable union of pairwise disjoint sets was vastly improved by Lebesgue who revolutionized the field of integration with his Lebesgue Measure. Lebesgue added three more conditions to the measure

1. It is translation invariant

2. Countable additivity when applied to disjoint sets.

3. Measure of interval(0,1) is 1

With this definition of measure , he observed that outer measure and inner measure of a sets for all subsets of R were not equal. Also m(S-R) =m(S) – m(R) was not applicable to all the subsets of R. He then introduced a class of sets called measurable sets , which closely parallels Caratheodory’s condition. So , the slick presentation of Caratheodorys condition in most of current books is nothing but a statement of measure of a set and its complement , m(E) + m(E’) = 1. The chapter then goes on in to discussing the properties of measurable sets which maintain their status under Countable additivity, Finite unions and intersections, Approximations by finite number of open intervals. The chapter ends with a detailed construction of a non measurable set invoking “Axiom of choice”. Do non-measurable sets exist ? Like a lot of stuff in math, that is the wrong question to ask. We do not seek existence of mathematical objects, like lets say a 26 dimensional object. What we are interested in math is the rules that such objects follow. In the case of non-measurable set too, if we accept the axiom of choice, it exists!!

**Chapter 6 : The Lebesgue Integral
**This chapter introduced the concept of measurable function and lebesgue measure. One immediately notices that measurable functions are nice objects which preserve their properties under various operations, primary being the limit of measurable functions is measurable. The building block of any measurable function is termed as simple function and one can define any measurable function as a limit of simple functions. The chapter goes on then show that every Riemann integrable function is Lebesgue integrable and the value concurs by either of the approach. Lebesgue in his work subsequently realized the extent of pathology permitted for a function to be Riemann integrable . His lemma that says, “a bounded function defined on a closed and bounded interval is Riemann integrable if and only if it is continous almost everywhere “, put an end to the quest of finding the extent of discontinuity permitted for Riemann integrable function to an end.

Lebesgue integral by its very definition cannot be taught quickly to a beginner . A Riemann integral can be intuitively explained away to any undergrad with the concept of partitioning/area under the curve/ etc. In contrast, the very definition of Lebesgue integral assumes that the student is aware of concepts like simple functions, characteristic functions, supremum for a set of functions etc. I think it is only after carefully going over the real analysis concepts from scratch that one can begin to understand Lebesgue integral.

The chapter then goes on to talk about Monotone Convergence Theorem (MCT)and Dominated Convergence Theorem (DCT) both of which are essentially used to swap limit and integral signs in relation to a sequence of functions and its limit. MCT is relevant to monotonically increasing sequence of non negative measurable functions while DCT is relevant to a sequence of Lebesgue integrable functions. DCT is a sufficient condition not a necessary condition to swap limits and integral sign. The chapter then talks about various types of convergence such as convergence in measure, uniform convergence, point wise convergence, almost sure convergence etc and tries to give an insight in to the linkages between these types of convergence.

**Chapter 7 : The Fundamental Theorem of Calculus
**This chapter takes a closer look at differentiation. It starts off with defining Dini Derivatives and stating that a function is differentiable at a point if the four Dini derivatives at c are finite and equal. Dini also observed that if a function f has a Dini Derivative that is either bounded above or bounded below , then f can be written as a difference of two monotonically increasing functions. Camille Jordan found a simple characterization of Dini’s statement using a concept called bounded variation.

Every grad student taking a course on Brownian motion comes across bounded variation. However often times , there is no time for the faculty to go over the historical context of bounded variation. Books such as these are immensely helpful in giving a context. This book makes the reader aware of the connection between Dini Derivative and Bounded variation and thus pours flesh and blood in to seemingly dry definitions.

Coming back to this chapter, the next section covers a very important property about monotonic continuous functions, i.e they are differentiable almost everywhere. This was proved by Lebesgue. Weierstrass belief that some will find a monotonic continous function that was nowhere differentiable function was conclusively laid to rest. A few years later, a husband and wife team of William Young and Grace Young published an independent proof that continuity is not needed. Bounded Variation MEANT Differentiable Almost everywhere.

It then moves on to the problems with original FTC and explains the necessary conditions to move around the problems.

Antiderivative part of FTC

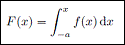
• When is a function integrable? - Measurable functions for which the integrals f+ and f- are finite

• If the integral exists, when can that integral be differentiated? - Always, almost everywhere

• When does differentiating the integral take us back to the original function? - If the function in the integrand is lebesgue integrable

Evaluation Part

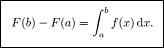
• When is a function differentiable ? - If the function has bounded variation , then it is differentiable almost everywhere

• If the derivative exists, when can that derivative be integrated ? - If the function is absolutely continous

• When does integrating the derivative take us back to original function ?  - If the function is absolutely continous

The biggest takeaway from this chapter is that

• Lebesgue Integral => Absolutely Continous

• Absolutely Continuity => Bounded Variation

• Bounded Variation => Differentiable Almost everywhere

The chapter ends with FTC stated using the concepts of Lebesgue measurable functions, Absolute continuity where the former is used to state the antiderivative part of FTC while the latter is used to state the evaluation part of FTC.

Chapter 8: Fourier Series

This chapter tries to answer the question that was asked at the very beginning of this book and the prequel to this book “A Radical Approach to Real Analysis”

“When does a function have a Fourier Series expansion that converges to that function?”

Lebesgue proved a theorem according to which, if a function f is integrable on [-pi, pi] , the Fourier series of f converges to f almost everywhere atleast in the cesaro sense of convergence. It is not something we would have wished for as it is not convergence on the entire interval but almost everywhere and the convergence is not uniform but in the cesaro sense. However it was a breakthrough as finally there was some mathematical condition based on which one could talk about Fourier Series convergence to the function that generated it.

I found this chapter very dense (it goes in to Banach and Hilbert Spaces) . I found it difficult to get past a few sections in the first reading. I will revisit this chapter at a later date and try to understand the application of functional analysis.

A related link to this post :  A Radical Approach to Real Analysis : Summary

Takeaway :

Even though there are books out there which are a potpourri of measure theory , lebesgue integral and probability concepts, none of them will give you a historical context to the development of ideas focusing exclusively on lebesgue measure.

Before attempting any study of axiomatic probability, this book needs to be read to get an idea of the relevance of lebesgue measure to EVERYTHING in probability. Once you understand the historical context, the appreciation of as simple as a uniform distribution function on (0,1) takes a new dimension altogether.