image

Laplace Transform is a very useful technique as it can be used in a ton of problems in various contexts. Here’s a random sample of the places where it’s use makes computations elegant :

  • Solving Difference equations in various Queueing configurations.

  • Renewal theory – Solving Key Renewal equation.

  • Solving specific type of ODEs.

  • Solving specific type of PDEs.

  • Computing convolution of two functions.

  • Moment generating function computations.

In most of the applied math books, all one sees is a table, tucked away in the Appendix, that lists out function and its Laplace transforms. Books such as these helps one see the real math behind the Laplace transform. The chapters are sequenced in an increasing order of difficulty. It starts off with the basic definition of the transform and discusses the convergence aspects. The following points are covered in the first chapter of the book

  • Laplace transformation exists for functions that have two properties, Piece wise continuity and Exponential order. However these properties do not characterize the entire class of functions (L) that have Laplace transform, i.e there are functions that do not satisfy one of these properties but still have a Laplace transformation.

  • Linearity property of Laplace transforms.

  • Necessary conditions for swapping the summation operator and Laplace operator.

  • Translation theorems.

  • Differentiation and Integration of Laplace transforms.

  • Using Partial fractions and applying Inverse Laplace transform to retrieve the original function.

The second chapter deals with functions that are a bit more difficult than the plain vanilla functions mentioned in the first chapter. Laplace transform for the following functions are derived :

  • Functions of the form tν where ν is a real number. Gamma function is introduced and a beautiful connection between Gamma and Beta function is explored.

  • logarithmic function

  • Periodic functions

  • Derivative functions

  • Dirac delta function

  • Bessel function

  • Error function

To understand the Laplace transform of the above functions, the chapter introduces more subtle ways of dealing with the convergence. For example the Laplace transform of Dirac delta function is defined in terms of Riemann-Stieltjes integral as the ordinary Riemann integral does not make sense. The applications covered in the chapter include:

  • Solving an ODE

  • Solving Systems of Differential equations

  • Solving Integro differential equations

  • Solving Differential equations with polynomial coefficients

  • Determining the asymptotic values of a function

  • Convolution

  • Solving Steady State equations

  • Solving Difference equations.

Along the way , I have learnt a nifty way to prove the following Euler’s equation. i.e. by taking Laplace transform on Beta function and using Convolution theorem

image

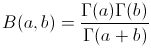
The first two chapters (114 pages) of the book give enough ammunition to problems in various contexts.

The difficulty level rises steeply from the third chapter onwards as the author takes the reader in to complex algebra. The third chapter contains all the relevant principles of complex algebra that are used in inverting a Laplace transform. Found it hard to follow as I had long forgotten complex analysis. Instead of going over at a 10,000 ft. view, I chose to go over the book on Complex Analysis by Howie. Having spent some time understanding the principles behind complex analysis, this chapter was a breeze. The chapter starts off with introducing complex numbers and techniques to evaluate limits, derivatives and integrals of complex functions. The techniques are very different from what one sees for real valued functions. Some of the key techniques to evaluate integrals of complex functions are

  • Cauchy integral formula

  • Cauchy residue theorem

  • Laurent series

  • Transform the integral to an integration around a contour.

In a sense, all of the third chapter’s content is geared towards giving enough background to work with inverse Laplace transforms.

The fourth chapter is on “Complex Inversion Formula”, a formula that uses contour integration to compute the inverse Laplace transformation. For a function having finite poles, the application of Cauchy residue theorem gives the inverse Laplace transform. It is a straightforward computation, once you are comfortable with complex analysis. However for a function with infinite poles, the problem is vastly more difficult. This chapter made me feel that inverting Laplace transform is more an art than science. Why do I feel that way ?Well, you have to choose the right kind of contours to encompass all the poles, prove that the function is bounded in a certain way and then use the Cauchy residue theorem.Using Cauchy residue theorem gives the right answer ONLY when one has ensured that all the prerequisites are taken care of(which I think is very tricky). After slogging through 150 pages of the book, I am kind of disappointed as I was expecting a magic technique that can be used to solve any inverse Laplace transform. Unfortunately such a method doesn’t exist. In any case, I will console myself that at least I can use contour integration for compute the inverse Laplace transform for simple functions. I think I should start looking around for a numerical procedure for inversion. The last chapter deals with using Laplace transforms to solve PDEs, most of them are standard PDEs.

image Looking at the basic formula for Laplace transformation, one might mistake it to be a trivial operator. The real math lies in cracking the inverse Laplace transformation of a general function. This book gives  a rigorous treatment of the Laplace operator and is probably one of the few books out there that give this kind of in depth treatment with out overwhelming the reader.