Data Structures and Algorithms using Python

There aren’t many Python books that talk about Data Structures. One of the reasons could be that Python provides a rich set of collections like list, dict, queue, set etc. that writing a new Data Structure might be unnecessary. That being the case, it is always helpful to know the time complexity of various operations in list, dict,etc. For some of the algorithms based on trees and graphs, there is no option but to build an abstract data structure to suit the problem one is trying to solve. This book discusses all types of data structures using Python.Even though the book uses Python and the code eats up a lot of paper in the book, there are bugs in several code fragments and there is no errata anywhere on the web. In any case, let me list down some of the points from the book. and certainly not on the author’s website.

Chapter 1 : Abstract Data Types :

This chapter introduces ADTs, a programmer defined data type that specifies a set of data values and a collection of well-defined operations that can be performed on those values. ADTs can be viewed as black boxes with the set of operations grouped in to four categories :

1. Constructors

2. Accessors

3. Mutators

4. Iterators

What are the advantages of ADT’s ?

• One can focus on solving the problem at hand instead of getting bogged down in the implementation details

• One can reduce logical errors that can occur from accidental misuse of storage structures and data types by preventing direct access of the implementation

• The implementation of the abstract data type can be changed without having to modify the program code that uses the ADT

• It’s easier to manage and divide larger programs in to smaller modules, allowing different members of a team to work on the separate modules

Common terms defined

• Collection : Group of values with no implied organization or relationship between the individual values

• Container : An ADT that stores and organizes a collection

• Sequence : Container in which the elements are arranged in linear order

• Sorted Sequence

The chapter describes a situation where one needs a bag ADT and then uses list to implement the bag ADT. In doing so, it explains the various things one needs to consider while implementing an ADT. Also there is a section that explains the details of implementing an iterator for an ADT.

Chapter 2 : Arrays :

Python has a built in collection object, list that can be used for a wide variety of tasks. There is one downside to it. The physical space allocation of a list is usually twice as large of the user defined declarative size. To work around this redundancy, the chapter defines Array in one and two dimensions using the ctypes module in Python. The chapter also gives a prototype for Matrix class that essentially builds on the 2D Array class. The main learning from this chapter is that list is not always the best data structure to use. Here is the Big-O efficiency for the most common list operations:

Chapter 3 : Sets and Maps

This chapter defines a set ADT and uses a list to implement this structure. I guess these elementary data structures are meant to give the reader some kind of practice in creating data structures. Somehow I felt that this chapter could have been easily clubbed with the previous chapter as there is really nothing new here.

Chapter 4 : Algorithmic Analysis

The Big-O efficiency for dictionary is :

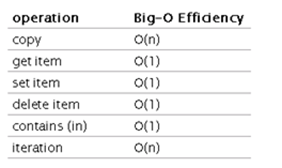
The Big-O efficiency for list is :

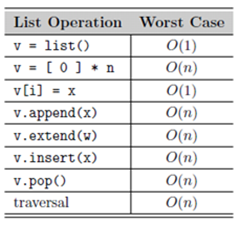
The above table cites the worst case time complexity of the operations. One can also compute the amortized cost. Amortized analysis is the process of computing the time-complexity for a sequence of operations by computing the average cost over the entire sequence. Amortized cost is not average case time. In the case of append operation for a list, the amortized cost is O(1) . The chapter ends with an example of Sparse matrix implementation.

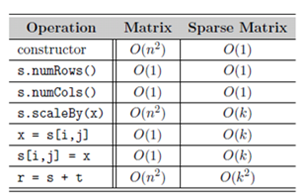
Chapter 6 : Searching and Sorting

Most of the ADTs need a search function. This chapter introduces binary search and improves upon the code from the previous chapters by making it a O(log n) operation vis-à-vis O(n^2). Another way to improve the search operation is sort the embedded data in the data structure. This chapter introduces bubble sort, selection sort and insertion sort algos. These sorting algos are then used in the ADTs explained in the previous chapters to store data in an sorted manner. The set ADT implemented in Chapter 3 is enhanced using binary search and sorted data structure to improve the efficiency for a few operations. The efficiency gains are shown below :

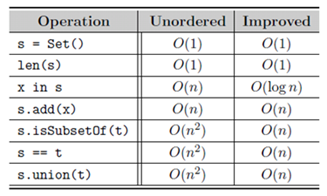
Chapter 6 : Linked Structures

If you want to implement a bag ADT, you can also use a linked list for the data storage. The only advantage of using Linked list is that it is O(1) for add operations as compared to O(n) for a list structure. Also if the data is very dynamic in nature, it is better to use linked list. The chapter has an implementation of single linked list and doubly linked list for a polynomial function that mimics all the operations of polynomials.

Chapter 7 : Stacks

This chapter provides a list based implementation and linked list based implementation of Stack data structure. Single linked list based implementation is better as the Big O efficiency for all the operations are O(1). Stack can be used in evaluating postfix expressions and the chapter shows basic algorithm for the same. The chapter ends with a nice maze puzzle that emphasizes the importance of the stack data structure.

Chapter 8 : Queues

One can implement a Queue ADT using list data structure. However the dequeue and enqueue operations are both O(n). Because the latter operations are O(n),alternate data structures are tried out such as circular linked list and linked list. In the case of circular linked list, even though the operations are O(1), there is a problem with the fixed size of the circular queue. The linked list overcomes the size limitation and provides O(1) efficiency for enqueue and dequeue. There is also an implementation of bounded priority queue using linked list based Queue. The disadvantage with bounded priority queue is, obviously the length of the Queue is fixed. In cases where such a restriction is natural, the bounded priority queue can be used to efficiently code the problem. Discrete event simulation can be done using Queue ADT. Skeleton code is given toward the ends of the chapter and the reader is encouraged to work through filling up the details in order to simulate a queue. Obviously the implementation is pretty naïve as it is meant for illustration purpose only. If you want to study lets say M/M/K priority type of Queuing system, the code needs to be substantially improved.

Chapter 9 : Advanced Linked List

This chapter talks about doubly linked lists , circular linked lists and multiple linked lists. 

Chapter 10 : Recursion

This chapter explains recursion using various examples, i.e

• Printing numbers in reverse

• Computing factorials

• Fibonacci sequence

• Binary Search

• Towers of Hanoi

• Tic-Tac-Toe

• Eight Queen problem

The above examples gives the reader good enough idea about the power of recursion. Personally I liked the Eight queen problem. I remember coding it some years ago , rather inefficiently in R. But coding the same in Python is so much more convenient from the collection objects in Python and the ADTs that can be built on top of them. I think the biggest learning from this book is a good programmer has a set of custom built data structures ready in his/her tool box to solve various problems.

Chapter 11 : Hash Tables

In a comparative based search algorithm, one cannot do better than O(log n). One way to improve the efficiency is by using Hash tables. By creating a explicit map between the key and the index value of its storage, the efficiency of search can be vastly improved. However not everything is Nirvana here. The biggest issue one must handle is that of “collisions”. The chapter gives a flavor of the various functions that can be used for linear probe to reduce clustering effects. The functions discussed are Modified linear probe, Quadratic probing and Double hashing. Also there is a mention of Rehashing technique. The efficiency of a hash table depends on the hash function, the size of the table and the type of probe used to resolve collisions. Pseudo code for Hash map ADT is provided. I have noticed a lot  of bugs in the code provided. The chapter ends with applying Hashmap ADT to displaying histogram.Again, the reader might not mistake that this is the real life implementation of a histogram. A histogram implementation in statistical packages involves pretty sophisticated math with FFT being the popular mode of implementing the histogram algorithm. One might be amazed to know that there are quite a few concepts that one needs to master to REALLY understand histograms, some of them being, “kernel density estimation”, “cross validation principle”, Fast Fourier Transformation etc. Sometimes I think there is no limit to the depths that you can plunge to understand anything. But the deeper you go, the better you understand things and the more confident you are , in solving real life problems.However there is always the risk of getting lost and I guess the art lies in knowing when to stop.

Chapter 12 : Advanced Sorting

Most of the sorting algorithms can be divided into two categories : comparison sort and distribution sort. In a comparison sort, the data items can be arranged in either ascending or descending order by performing pair wise logical comparisons between sort keys. The pairwise comparisons are typically based on numerical order or lexicographical order. A distribution sort, on the other hand, distributes or divides the sort keys in to intermediate groups or collections based on the individual key values. This chapter begins with merge sort, a recursive sort procedure which has O(n log n ) efficiency. It is followed up with a discussion on Quick sort, that has an average efficiency as O(n log n) but O(n2) in the worst case. What algo is used in Python list data structure ? As per the book, quick sort was followed in earlier versions but the newer versions combine insertion and merge sort algorithms. By this point in the book, 5 sorting algorithms are covered, bubble, selection , insertion, merge and quick sort. The first three have a worst case time of O(n2) while the merge sort has a worst case time O(n log n). The quicksort, the more commonly used algorithm in language libraries, is O(n2) in the worst case but it has an expected or average time of O(n logn). In a comparison based sort, one can do no better than O(n log n).

The chapter introduces RadixSort algorithm that drastically cuts down the sorting time for certain kind of contexts. It is a distributive sort algorithm where the values are distributed in to various bins and regrouped from the bins in such a way that after some iterations, the resulting list is a sorted list. There are also insertion sort and merge sort algorithms to data stored in the form linked lists. The insertion sort algorithms used with linked lists is O(n2) in the worst case whereas merge sort is O(n log n).

Chapter 13 : Binary Trees

Tree structure is introduced by defining the following terms

• Nodes

• Edges

• Root Node

• Path

• Parent Node

• Child Node

• Interior Nodes

• Leaf Node

• Subtree

• Depth of a Node

• Height of a tree

• Width of a tree

Binary Trees are defines and explained via rich visuals. Four kinds of tree traversals are mentioned, i.e Preorder Traversal, Inorder Traversal, Postorder Traversal, Breadth-First Traversal. Heaps are introduced in this section with min-heap and max-heap properties. Python code for max-heap is provided. Like many other codes given in the book, the code has a few bugs. Bounded priority queue can be implemented via Heaps. Here is the comparison for various implementations

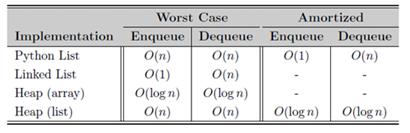
The logical sorting in this context, heap sort is a trivial extension of heaps. The chapter ends with a modified version of heap sort that is an inplace sorting algo.

Takeaway :

Data Structures + Algorithms = Programs. This book talks more about Data Structures and less about Algorithms.  The book can be useful to a Python programmer who wants to understand Big O efficiencies of various inbuilt collection objects in Python. In the process, one will inevitably realize there is a need to built Abstract Data Types to implement various algorithms.