Algorithms–Review Part I

Part I - Fundamentals

The first part of the book creates the necessary background for the reader to understand the various algorithms discussed in the book. The book implements all the algorithms in Java. Its not a problem if you are rusty with Java. The authors give some basic crash course on the language, just enough to understand all the algorithms. I have forgotten Java long back. I think it has been a decade since I have coded any Java program. However the code and the commentary for the code is crystal clear thus making it is easy for any non-java reader to follow the code and implement in a language of their choice. There are two essential aspects that are discussed in the first part of the book. First, it explains the main data structures like Bags, Queues, Linked lists, Doubly linked listed that are essential building blocks for all the algorithms in the book. Secondly, it explains the concepts behind analyzing the performance of an algorithm. When I look at these concepts, I think these need to understood just once and they are yours for lifetime. Basic principles of performance analysis are described in detail and I guess they ensure that every time you come across an algorithm, the first question that typically will pops up in your mind  is, “what’s the order of running time ?” . Answering this question allows one to connect with various algorithms that have similar running time. For example FFT algorithm is of O(N log N). Well, FFT achieves N log N by the same divide and conquer method that a merge sort algorithm uses.

Part II – Sorting

All sorting algorithms can be categorized in to two types. The first type of algos are “in-place” sorting algos and second type are the ones that need extra space. The section starts off by discussing elementary sort algos such as selection sort, insertion sort and shell sort. The running time for selection sort and insertion sort is quadratic whereas shell sort is O(N3/2). Once these elementary algos are dealt, the book moves on to discussing merge sort and quick sort. Both have linearithmic running times. There are two versions of Merge sort discussed in the book – the top down merge sort as well as bottom up merge sort, the usage depending on the context and need. Merge sort is a stable sorting algorithm and but it is not optimal with respect to space usage. The book then talks about Priority queues that are fundamentally different data structures. In all the previous sorting algos, the storage is typically an array and there is no specific structure in the array. In Priority queues, the keys are stored in an array but with a certain structure for the array. Even though the data is stored in an array, the structure is a tree structure.

The chapter on priority queues starts off with a practical problem of computing a summary statistic for a data stream.There are applications where keys are processed not necessarily in an ordered format and not necessarily all at once. Basically you process a few data items , then process the items with the largest key or smallest key and then insert new data items. Think about a stream of data where there is a need for random inserts and random delete maximum or delete minimums operations from a random stream of data. A concrete example is one where there are large number of strings that represent transactions and the problem is to keep the top M transactions by amount. Sorting is ruled out as N is very large. Store M largest seen so far is one approach but this fails if M is very large. A client that uses elementary implementation faces O(NM) in time , O(M) in space. Unordered Array based implementation is poor as insertion is O(1) but deletion is O(N). Ordered Array based implementation is poor as insertion is O(N) and deletion is O(1). So, what’s the way out of this linear time insertion problem ? The solution lies in using a different data structure, the heap. A client that uses heap-based implementation faces O(N log M) in time and O(M) in space.

The book discusses two variants of Priority Queues, i.e. MaxPQ and MinPQ, the former always creates a parent node whose key is greater than that of children’s keys and the latter creates a parent node whose key is always less than the children’s keys. Using two helper operations called sink and swim operations, priority queues become very efficient data structures that operate on a linearithmic running time. Extending the concept of priority queue gives another sorting algorithm called the heap sort. The classical heapsort algorithm was invented by J. W. J. Williams and refined by R. W. Floyd in 1964. Heap sort has two phases. First phase is the heap construction and second phase is the sort down procedure. The sort down procedure is where most of the work gets done. The procedure is similar to selection sort but is very efficient because of heap structure. The true advantage of heapsort is that it does not require additional space. It does inplace sort and it is linearithmic. The downside to heap sort is its poor cache performance and hence it is rarely used in modern applications. The book has a lot of interesting programming problems. It all depends on how much time and effort you can invest in to the book. One of the problems I liked is the use of Priority Queue to compute Kendal’s tau.

Part – III: Symbol Tables

The third part of the book covers Symbol table, the building block for any search algorithm. A symbol table is a term used to describe an abstract mechanism for saving information(value) and retrieving the information by specifying a key.Symbol tables are sometimes called dictionaries or indices. Specifying a key and value can be done in umpteen number of ways. But it is important that one does it in an efficient manner. One easy way is to store two arrays one storing the key and the other storing the value. This is inefficient if the data involves random “puts” and “gets”. Any “get” becomes is linear time and hence becomes an inefficient algo. The two important operations for a symbol table are insert() and search().  Several symbol table comparisons take advantage of the order among the keys. Once there is an order amongst keys, the basic API involving put and get can be expanded to many other operations like min, max, floor, ceiling, rank, select, deleteMin, deleteMax, range etc.

The clients for Symbol Tables typically share the following characteristics

• Search and insert operations are intermixed

• Number of distinct keys is not small

• Substantially more searches than inserts are likely

• Search and insert patterns, through unpredictable are not random

The first symbol table implementation in the book is via unordered linked list. It is obvious that insert is O(1) whereas search is O(N). Subsequently the chapter implements ST using ordered linked list. In this case, using a rank procedure the search cost becomes logarithmic but the insertion cost remain linear time operation. After these elementary implementations, it is abundantly clear that these don’t' scale. A fundamentally different data structure is needed to handle big data. Binary search trees are introduced in the next section of the book to address slow insertion issue for the elementary implementations

The best thing about Binary search trees is that insert and search operations are logarithmic in time. In fact it is is 1.39 log N. Delete operation is the complicated operation amongst all. In BST all operations take time proportional to the height of the tree. So, except for the worst case scenario, BST is much better than elementary implementations. In order to guarantee logarithmic time search and insert operations for the worst case scenario too, the book introduces a new data structure, a tweak of binary search trees that allows 2 keys to be at a node. These are called 2-3 trees and all the worst case situations are efficiently handled by 2-3 trees. However implementing 2-3 trees is done by RedBlack trees. Every Red Black tree has a one to one relationship with a 2-3 tree. The reason for it being called  a Red Black tree : the node carries a color attribute that tells whether they belong to the same node in the corresponding 2-3 tree. The implementation details of a Reb Black tree is complicated, especially the delete operation. However if you sweat it out and implement it, you get a data structure that guarantees logarithmic performance in the average case as well as the worst case.  These data structures are like high powered tools in your tool box to attack big problems. One of the interesting problems mentioned in the book is the reverse index for a big data set. If you have to code from scratch and not use some off the shelf functions, the best way to build an inverted index is to use Balanced Search trees. The last part of this section talks about a data structure that uses hashing to maintain key value pairs. Two types of data structures are discussed, first is the Separate Chaining Hash Symbol table and second is the Linear Probe Hash Symbol table. In the former you maintain separate symbol table takes for every hash key. In the latter , you maintain a single symbol table and manage all the collisions.

The following table summarizes all the algorithms discussed under symbol tables. As one can see, the more sophisticated data structure that one uses, the better handle one gets on the running times.

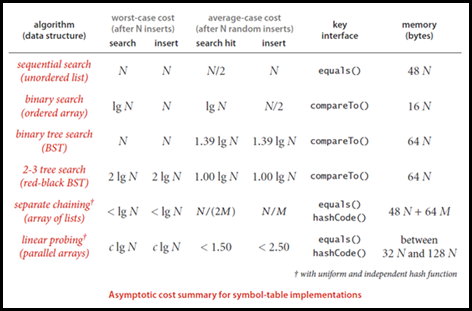
The first three parts of book takes up 500 pages of this massive 1000 page book. The other parts of the book cover algorithms based on graphs and strings. Hopefully will summarize the subsequent 500 pages of this book someday. The highlight of this book is “rich visuals” that explain the nuts and bolts of algorithms. I guess the natural progression for the reader would be to overlay a OOPS class hierarchy over the several individual classes mentioned in the book.