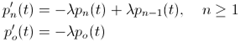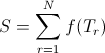If one tries to read some historical developments behind Brownian motion, there is no dearth of material on the web. There are also entire books written that trace the events that lead to Brownian motion and how it was used in various domains. However for the Poisson process, there is a paucity of literature that traces the history. I stumbled on to a note by David Strirzaker that recounts the history behind Poisson processes. I will paraphrase a section from the paper deals with the history.

clip_image002 Abraham De Moivre

In 1718 Abraham De Moivre published The Doctrine of Chances in which he derived Poisson density form as a limiting distribution of a Binomial distribution under a specific condition. However he did not note, or use, the fact that this yields a proper probability distribution.

clip_image004Siméon Denis Poisson

In 1837, D. Poisson showed that the limiting form of Binomial distribution indeed is another probability distribution.

clip_image006Robert Leslie Ellis

In 1844, Robert Ellis contributed a paper to the Cambridge Mathematical Journal in which he considered the random process in which events are separated by times which are independent and exponentially distributed. He found the distribution of the sum of such exponentially distributed variables and established a form of Central Limit Theorem for the sum of independent random variables in general. However, he did not produce the Poisson distribution or the important properties of the process.

Close of 19th Century

Poisson’s book was widely read, and the Poisson limit of the binomial cropped up in an amazing array of contexts towards the close of the 19th century.

  • Counting blood cells

  • Thunderstorms

  • Theory of gases

  • Earthquakes

  • Incidence of deaths from horse kicks in Prussian Cavalry

  • Paper by Simon Newcomb was perhaps the first paper that focused on application of the Poisson distribution to data

Opening years of 20th Century

Several reports also started to appear in the early years of 20th century, some of them being

  • Theory of gases

  • Particles in suspension

  • 1905 : Charlier noted that the Poisson probabilities satisfies a special kind of differential equation

  • 1907 : W.H.Grinsted used the same model as Robert Ellis to describe telephone traffic problems

However, the general essence of all the results is essentially static and tabular. There is no sense of a process, nor are the characteristic properties of the Poisson process were made explicit.

1909 – Fog clears

THREE separate scientific and mathematical investigations each produced the Poisson process with its essential characteristics:

image

clip_image004[5] Hans W Geiger   clip_image006[5] Ernest Rutherford

clip_image008 Harry Bateman

Hans W Geiger and Ernest Rutherford developed what is now famously knows as Geiger counter to record α particles. They asked Bateman to formulate a mathematical description of this random process. He produced the family of equations

image

whose solutions are of the form

clip_image001

image Norman Campbell

Norman Campbell noted that a great many processes, previously regarded as continuous process should now be described as discrete stochastic processes. Classic examples are provided by photons and the passage of electrons across thermionic valves. Inevitable in calculating the effects of such processes one must consider random sums of the form

clip_image003

Where T1,T2, are in effect the events of a Poisson process and N has a Poisson distribution. The theorem which supplies the moments and moment generating functions of S, and later generalizations has thus come to be known as Campbell’s theorem.

image

clip_image007**
Agner Krarup Erlang**

In 1909, Erlang, who worked for the Copenhagen telephone company for twenty years, was looking at delays and congestion in telephone systems. He supposed that the process of incoming calls had independent increments and constant rate, and hence naturally he derives the Poisson process.

It seems reasonable therefore to assign 1909 as the birthdate of Poisson process. After this date there is an explosive growth in the development and bibliography of the Poisson process and its generalizations and relations. However, for many years the development is far from straightforward. Results were constantly being rediscovered in different places, and names and notation were not standardized for many years. Paradoxically, it is because it is so universal in its applications that the early history of the Poisson process is so confused. In the first part of this century, its properties were being studies and developed by biologists, ecologists, engineers, and physical scientists of all kinds. These published in several different languages, and in a variety of journals that were not widely disseminated.

1930s

As usual rational analysis had to wait until the mathematicians joined in, which they did in the early 1930s. Key papers include that of Kolmogorov in 1931, with others by Feller and Khinchin.

clip_image009 Kolomogorov   clip_image011 Khinchin

As with many other things in probability, a key figure in this is William Feller. Not only did his book make the Poisson process pivotal and widely accessible, but he may have been the first to refer to “The Poisson Process” in print, in 1940

clip_image013 William Feller

NOW

In today’s world, especially in the field of finance, the Poisson process is everywhere. If you want to model the price process with jumps, the least you can do is to use a non homogenous Poisson process. In this big data world, analyzing trade data at an aggregate time scale is not enough. The availability of data at a high frequency scale makes it imperative to analyze the irregularly spaced trades as a marked point process and here again the Poisson is immensely useful so that one can build an elementary model and iteratively add features.

In any case, it is always helpful to know the people behind a stochastic process so that one can put a face behind the core theorems and characteristics of the process.