The Misbehavior of Markets : Summary

Crisis hits financial markets at regular intervals but the market participants keep assuming that they “understand the behavior” of markets and are in “total control” of the situation until the day things crash. There is an army of portfolio managers, equity research analysts, macro analysts, low frequency quants,derivative modeling quants, high frequency quants etc., all trying to understand the markets and trying to make money out of it. Do their gut /intuitive/quant models come close to how the market behaves ?.

I had bought this book in May 2008 assuming that I will read the book on some weekend. Somehow that weekend never came. Years flew by. For some reason I stumbled on to this book again and decided to read through this book. In the last 6 years I have read many books that have highlighted the inadequacy of quant models to capture market place reality. Before going through the book , I had a question – “How is this book different from all those model bashing books?”.

Here is a list of other questions that I had before reading the book :

• Gaussian models do not predict the kind of randomness that we see in our markets. I had anticipated that the book is going to be Gaussian bashing book. What’s the alternative to Gaussian models?

• Some practitioners have included jumps in to the usual Brownian motion based models and have tried to explain various market observed phenomena like option skew, volatility jumps, etc. What does the book have to say about Jump modeling? Are Jump processes good at only explaining the past or Can they serve as a tool for better trading and risk management decisions ?

• Are fractals a way of looking at price processes?  If so, how can one simulate a price process that is based on fractal geometry ?

• What are the parameters of a fractal model?

• How do you fit the parameters of a fractal model?

• Can one put some confidence bounds on the fractal model parameters? If so, how?

• Why hasn’t the idea taken off in the financial world, if the fractals are ubiquitous in nature?

• Why are academics reluctant to take a fractal view of the market?

• Why are quants reluctant to take a fractal view of the market?

• What is Mandelbrot’s view of financial modeling and risk management? Can risk in the financial markets be managed at all, given the wild randomness that is inherent in the market ?

This book answers many more questions than those that I have listed above. Let me try to summarize briefly each of the 13 chapters of this book:

Risk, Ruin and Reward:
This chapter gives a preview of the basic idea in the book. Fundamental analysis, technical analysis and the more recent random walk analysis all fail to characterize the market swings. However there has been a massive reluctance to move away from such kind of mental models. Partly the system of incentives is to be blamed. The authors say that the goal of the book is to enable readers appreciate a new way of looking at markets, a fractal view of the market. The background to this view is put forth in terms of five rules of market behavior.

1. Markets are risky

2. Trouble runs in streaks

3. Markets have a personality

4. Markets mislead

5. Market time is relative

At the outset the authors say that this is not a “how to get rich” kind of book but more of a pop science book.

By the Toss of a Coin or the Flight of the Arrow:

The authors introduce “types” of randomness in this chapter. There are two types of randomness, “mild” and “wild”, the former is akin to tossing a coin and the second is akin to a drunk archer hitting a target. The former is the Gaussian world where things are normal and significant deviations from the mean are almost 0 probability, whereas the latter is the Cauchy distribution world where averages don’t converge and the deviations appear so big that the term “average” doesn’t make sense. Using these two distributions, the authors give a glimpse in to the spectrum of randomness types possible. Financial research, tools and software in today’s world are predominantly built around with the assumption of mild randomness. However the world seems to be characterized by “wild” randomness.

Bachelier and his Legacy:

The authors dig in to the history and recount Bachelier’s life. He was the first person to apply mathematical principles to stock market. He is credited for viewing the price process as an arithmetic Brownian motion. This view was never appreciated by his contemporaries. Almost 50 years later, Bachelier’s paper was picked up by Samuelson, a professor at MIT. Samuelson was a wizard at mathematics and he was on a course to make economics a quantitative discipline. Samuelson and others like Fama( University of Chicago) worked on Bachelier’s view of the market, improved it and applied to a whole host of areas like portfolio management, risk assessment, etc. Castles were being built on sand and these castles were multiplying too in different locations. Almost no one wanted to verify the basic assumption of continuous Brownian motion process.

The House of Modern Finance:

The authors talk about three pillars of modern finance that is taught all over the universities, i.e. CAPM(Capital Asset Pricing Model), MPT(Modern Portfolio Theory),BSM( Black Scholes and Merton framework). The first was developed by Markowitz, the second by Sharpe and the third by Fischer Black,Myron Scholes and Robert Merton. CAPM dealt with dishing out portfolios to investors based on their risk appetite. MPT simplified CAPM and dished out a market portfolio, that later became the bedrock for index funds, and BSM was a framework for valuing options. The crux of each of the pillar goes back to Bachelier’s work. No one was willing to criticize the component of Brownian motion that was used in all these frameworks. There was a rapid adoption of these tools in the industry, almost blind-faith obedience to all these models. Soon however financial crisis brought semblance amongst investors and traders and some of them began to develop strong dose of skepticism over these models. Warren Buffet, once jested that he would create a fund so that academicians could keep teaching these three pillars of modern finance to people so that he would make money by trading against them.

This book was written in 2004 but did it stop people from using mild randomness models for the market ?. No. The ever wide spread usage of Gaussian copula model before the full fledged onset of subprime crisis is a point in case that the castles of air built on mild randomness are still being used. VIX index is a nice example of how people are shying away from using the volatility based on underlying. VIX uses option prices to get an estimate of ATM volatility. All said and done, it does use GBM. So, it is a “FIX” too.

The Case against Modern Theory of Finance:

The authors use this chapter to set the stage for the next part of the book, i.e. way to understand different types of randomness (mild, wild and everything in between). The following are some assumptions that make all the academic theories that have been developed till date, very fragile. They are

• People are rational and aim only to get rich

• All investors are alike

• Price change is practically continuous

• Price changes follow a Brownian motion

Look at the daily returns of the Nifty total returns index. They are nowhere near close to that generated by a Geometric Brownian motion process that is assumed in finance literature. The second visual has been generated with the assumption of GBM with observed nifty volatility looks too regular as compared to the reality.

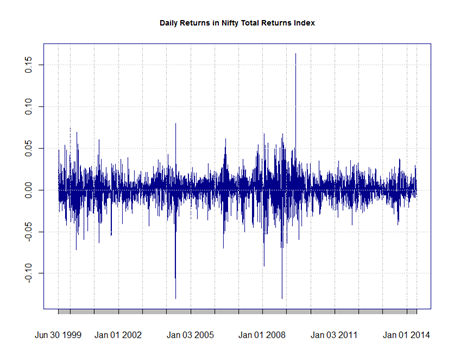
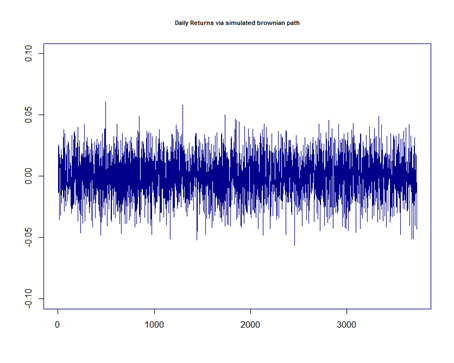
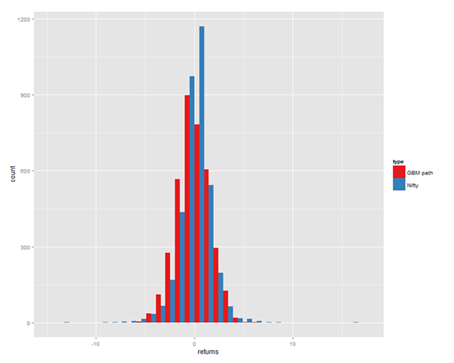
The above picture compares the frequency counts of returns for GBM path and Nifty. One can see that blue bars are all over the place as compared to GBM counts. A few pictures relating to price changes make it abundantly clear that the returns do not follow a GBM for equity, forex, commodity markets. Since various crisis have hit the markets, many researchers have observed CAPM anomalies such as P/E effect, January effect, Market-to-Book effect that do not make sense in a CAPM world. The authors say that the most saddest thing is that when things do not fit the model, the model is tweaked here and there to explain the market behavior. Some of the tweaks that have been created are

• Instead of one factor, introduce many factors that explain the returns

• Instead of constant volatility, incorporate a conditional equation for the volatility

The authors vehemently argue that these are all adhoc fixes. All are variations around Gaussian model and hence are fundamentally flawed.

Turbulent Markets: A Preview

The authors make a case for using “turbulence” as a way to study price processes. This chapter gives a few visuals that can be generated via multi fractal geometry.

Studies in Roughness:

The authors use extensive set of images to convey the basic properties of a fractal. A fractal can be identified based on three characteristics

1. Initiator – Classical geometric object , i.e. a straight line, triangle, solid ball etc.

2. Generator – A template from which fractal will be made.

3. Rule of Recursion – This decides the way fractal is repeated

The authors generalize the Euclidean dimension and introduce fractional dimension. This concept is made clear via examples and pictures. The concept of dimension is based on the shrinking ruler length and the increasing measurement length. In most of the phenomena that authors have researched, they have found a surprising convergence for the logarithmic ratio of the two quantities, ruler length and measurement length. This ratio is summarized as a parameter for the scaling law that is put forth in the book.

The Mystery of Cotton:

This is one of the most fascinating chapters of the book. It deals with connection between fractal geometry and cotton prices. There are three pieces to this connection

1. Power laws

2. Power laws in economics

3. alpha stable distribution

Combining these three aspects, Mandelbrot plots the change in cotton prices vs. frequency count on a log-log scale and finds a remarkable pattern across time scales. He finds that the cotton prices obey an alpha stable distribution with alpha being -1.7. This piece of evidence was stubbornly resisted by many academicians. During the same time period, there was a massive wave of CAPM, MPT, BSM that was sweeping through academia and the industry. Amidst this wave, Mandelbrot’s cotton price analysis did not find the right traction.

Here is the log log plot for up move vs. its frequency, down moves vs. its frequency for Nifty total returns index.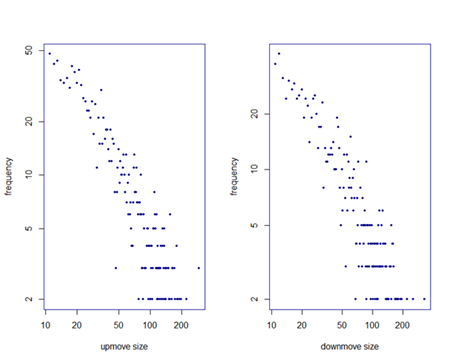

The slope for the above graphs is approximately -1.1. What do the above graphs say? The frequency of up moves and down moves follows power law. A great many small jumps and small gigantic jumps is what characterizes NIFTY. The above is based on daily returns. One can do a similar analysis at a 5 min interval scale or 15 min interval scale and see that this power law relationship scales across time intervals.

Some people might not believe that such a scaling law exists among financial markets. One simple test that the author recommends is : Take an intraday transaction price data, remove the x axis labels and y axis labels. If you show this graph to someone, they might easily mistake it to be a chart based on closing prices. In physics there is a natural boundary between the laws. The laws that work on macroscopic level are different from that of the laws that work on microscopic level. The scale matters in such field. In finance, there is no reason for such a time scale to exist. Any model you build should take in to consideration this scaling aspect of financial time series.

How does one interpret the value of the slope –1.1 ? It turns out that the slope value for wild randomness is close to -1 ( Cauchy distribution) and slope value for mild randomness is -2 ( coin tossing context). For Nifty, the value is close to –1, i.e wild randomness. Well, one can only wish a dose of good luck to all who are trying to make money in such wild markets.

Long Memory, from the Nile to the Marketplace:

 H.E.Hurst

The authors narrate the story of H.E.Hurst , an Englishman, a chief scientist at Cairo who immersed himself in a particular problem, i.e. forecasting the flooding intensity of river Nile. Because the amount of flood varied from year to year, there was a need to create “century storage” to stockpile water against the worst possible draughts. This task was assigned to Hurst. As he began investigating the data, he found that the yearly rainfall was Gaussian. The problem however was with the “runs”. He found the range from highest Nile flood to lowest widened faster than what a coin-tossing rule predicted. The highs were higher, the lows, lower. This meant that not only the size of the floods, but also their precise sequence matter. Hurst went on a data collection exercise and collected all sorts of data without any preconceptions. He looked through any reliable, long-running records he could find that were in any way related to climate, for a total of fifty-one different phenomena, 5915 yearly measurements. In almost all cases, when he plotted the number of years measured against the high-to-low range of each records, he found that the range widened too quickly – just like the Nile. In fact, he found as he looked around the world, it all fit the same neat formula : the range widened not by a square-root law as coin-tossing, but as a three-fourth power. A strange number, but it was , Hurst asserted, a fundamental fact of nature.

This “Nile flood” example is one that is very often quoted to illustrate “Long memory processes”. So, in simple words, these are time series where the dependency dies down very slowly. If you plot the autocorrelation plot, the series dies down slowly as compared to any stationary process. One can easily get the Nile data from the web. This plot shows that yearly flood data is nearly normal but the second plot shows that ACF decays very slowly. The third plot shows a linear relationship between log range and log duration and the slope of the line is estimated as the Hurst coefficient.

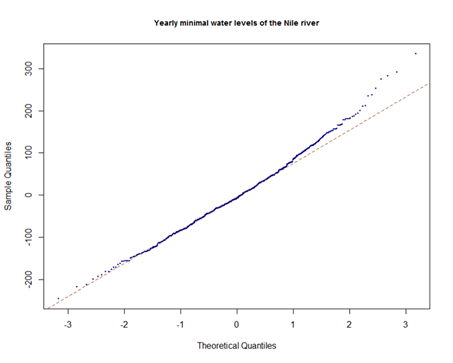
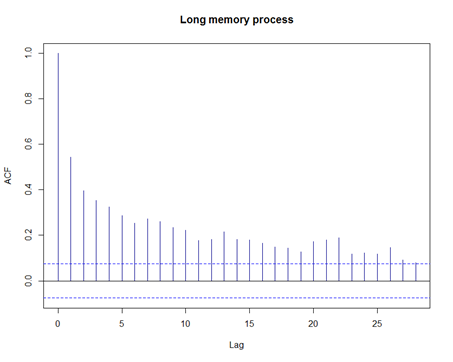
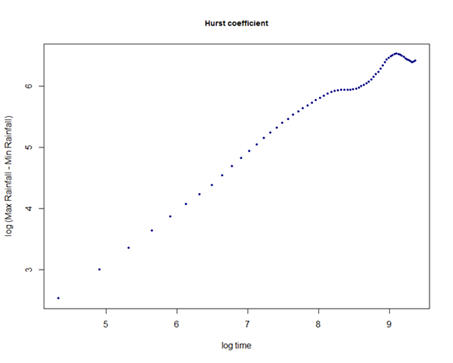
In a chance conversation with a professor at Harvard, Mandelbrot starts working on long memory processes. To paraphrase the author here,

The whole edifice of modern financial theory is, as described earlier, founded on a few simplifying assumptions. It presumes that man is rational and self-interested. Wrong, suggests the experience of the irrational, mob-psychology bubble and burst of the 1990’s. A further assumption: that price variations follow the bell curve. Wrong, suggest the by-now widely accepted research of me and many others since the 1960s. And now the next wobbles: that price variations are what statisticians call i.i.d independently and identically distributed – like the coin game with each toss unaffected by the last. Evidence for short-term dependence has already been mounting. And now comes the increasingly accepted by still confusing evidence of long-term dependence. Some economists, when thinking about long memory, are concerned that it undercuts the efficient market hypothesis that prices fully reflect all relevant information; that the random walk is the best metaphor to describe such markets; and that you cannot beat such an unpredictable market. Well, the efficient market hypothesis is no more than that, a hypothesis. Many a grand theory has died under the onslaught of real data

Mandelbrot incorporates this dependency in his fractal theory and denotes it as H, the Hurst coefficient. For a Brownian motion, H equals ½ and for any other persistent process, H tends to fall between ½ and 1. The more the persistence, the more H will be close to 1. If H is smaller than ½, then the process is in a mean reverting mode. With this context, the authors introduce “Fractional Brownian motion”.

Noah, Joseph and Market Bubbles

The title of the chapter is meant to aid readers to quickly recall the two effects that are present in the financial markets; first characterized by the sudden jumps in the prices and second characterized by the long memory nature of prices. The authors use two stories from Bible and they probably resonate with someone who is familiar with Christian mythology. The takeaway for me is that Mandelbrot’s theory is a combination of two parameters, “alpha” that takes in to consideration the scaling law and Hurst coefficient that tries to characterize the long term memory of the price process. The wildness that characterizes markets can be described in two words – “abrupt change” and “almost-trends”. These are the two basic facts of financial market, the fact than any model must accommodate. They are two aspects of one reality. Mandelbrot also mentions about a test to tease out two effects, a non parametric test called “rescaled range analysis”. But in some cases the two effects are closely related and teasing out the two effects becomes challenging. The chapter also talks about the interplay of Noah and Joseph effect in creating financial crisis at regular intervals.

The Multifractal Nature of Trading time

This chapter combines the two aspects, dependency and discontinuity and mixes it with trading time, a concept explained in this chapter. This combination results in a Multifractal model. Honestly I need to work with this model to get more understanding about the way it works. Pictures do convey a good idea about the model but my understanding as of now is very hazy.

Ten Heresies of Finance

This chapter lists a collection of facts that authors have found useful in their work

1. Markets are Turbulent – Two characteristics of turbulence are scaling and long-term dependence. These characteristics are found in a number of examples from natural to economic phenomenon

2. Markets are very, very risky – More risky than the standard theories imagine: Average stock market returns mean nothing to the investor. It is the extremes that matter. That’s where most of the money is made or lost. This is what explains the equity risk premium puzzle.

3. Market “Timing” Matters Greatly – Big Gains and Losses Concentrate in to small Packets of Time : Ignore your broker’s advise that their clients should buy and hold. Most of the returns(positive or negative) are made in small concentrated time units.

4. Prices often leap, not glide – That adds to the risk: Continuity is a common assumption and when you backtest a strategy, it is likely that your entry and exit points might seem perfect. The only problem is, in reality, the price jumps and by the time you are in the market based on your entry point, the market has squeezed out a significant proportion of the profit from the proposed strategy. The mathematics of Bachelier, Markowitz, Sharpe and Black-Scholes all assume continuous change from one price point to the next. All the assumptions behind them are false. The capacity for jumps, or discontinuity, is the principal conceptual difference between economics and classical physics. Discontinuity is massively profitable for market makers. You got to model it and incorporate it in your strategy.

5. In Markets, Time is Flexible – The crux of fractal analysis is that same formulae apply to any scale , be it at a day scale, or an hour scale or a monthly scale. Only the magnitudes differ, not the proportions. In Physics, there is a barrier between subatomic laws of quantum physics and the macroscopic law of mechanics. In finance, there is no such barrier. In finance, the more dramatic the price change, the more the trading time-scale expands. The duller the price chart, the slower runs the market clock

6. Markets in All Places and Ages Work Alike – This is like throwing away localized market microstructure studies away!

7. Markets are inherently uncertain and Bubbles are inevitable - This section has a very good analogy, comparing “land of ten thousand lakes with a neighborhood called Foggy bottoms” to “trading world”. Very interesting analogy.

8. Markets are deceptive – Be aware of the problems with just going with technical analysis.

9. Forecasting Prices may be perilous, but you can estimate the odds of future volatility – A 10% fall yesterday may well increase the odds of another 10% move today – but provide no advance way of telling whether it will be up or down. This implies correlation vanishes despite of the strong dependence. Large price changes tend to be followed by more large changes, positive or negative. Small changes tend to be followed by more small changes. Volatility clusters. This means that at least you have some handle on it. However you cannot predict anything with precision. Forecasting volatility is like forecasting the weather. You can measure things but you can never be sure enough. This section also mentions about “Index of Market Shocks”, a scale that is used to measure financial crisis.

10. In Financial Markets, the idea of “Value” has limited value – All value investors will have a shock treatment after reading this section. Value is a slippery concept and one whose usefulness is vastly over-rated

The authors end this chapter with the following quote:

The prime mover in a financial market is not value or price, but price differences, not averaging but arbitraging

**
In the Lab**

The last chapter begins with mentioning academicians, quants and traders who are working on fractals in finance.

Richard Olsen

For more than two decades Olsen and his team ( Oanda.com) of mathematicians have been analyzing high frequency data. The authors narrate the team’s history and their work. Olsen started his firm after having a sense of frustration with the way financial models have been modeled and used. The sheer lack of understanding in to financial markets makes him get up every day and head off to do his research. Olsen firmly believes that world is a fractal and hence uses all the techniques from Mandelbrot’s theory to understand and trade in the markets. More specifically, he uses multifractal analysis that rests on the assumption that “trading time” is different from “clock time”.

Jean-Philippe Bouchad

Capital Fund Management, a hedge fund based out of Europe uses a mix of statistical arbitrage and multi fractal analysis for their trading strategies. The fund firmly believes in scaling by power law and long-term dependence and hence uses a different kind of portfolio management techniques. They call it “generalized efficient frontier” where they focus only on the odds for a crash and their scaling formula minimizes the assets in a portfolio crashing at the same time.

Edgar Peters

Edger Peters, another asset manager believes in fractals and has written two books on them. However he does not use them in his funds as he says that his conservative clientele were not interested. In the hindsight of so many crisis that have happened, conservative clientele should have been more than interested in fractals as it comes close to actually explaining the market behavior.

Mandelbrot says that very little work has actually been done in using fractals in finance. He lists the following areas where fractals can truly play a great role

• Analyzing investments

  • There are so many types of numbers that are seen in the trading/investment world, p/e , volume, EBIDTA,PAT, etc. However when it comes to measuring risk,the industry’s toolkit is surprisingly bare. The two most common tools are volatility and beta of the stock. These two numbers are used again and again everywhere. The assumption behind these numbers is bell curve. How could it possibly be that one and the same probability distribution can describe all and every type of financial asset ? Mandelbrot says that finance today is in a primitive state. Its concepts and tools are limited. The work on scaling, long term memory has just begun. There are many methods to compute Hurst coefficient but no major work has been done show the robustness of methods

• Building Portfolios

  • CAPM or its variants are all driven by mild randomness assumptions. In 1965, Fama showed that one needs a far greater set of stocks in a portfolio if one makes wild randomness assumption. There is a need for creating a new, correct portfolio theory. Today, building a portfolio by the book is a game of statistics rather than intelligence. In any case, Mandelbrot suggests that every portfolio manager should simulate price series using Monte Carlo methods and test their ideas. Using the methods from the book, one can easily simulate a series based on multifractal geometry and then test out whatever strategy one wants to test out.

• Valuing options

  • This is another area that cries for guidance. Black schools theory is just that, a theory that makes the very existence of an option redundant. If one can perfectly replicate an option, aren’t options redundant? The observed volatility smile is corrected using a range of fixes such as GARCH, Variance gamma process etc. In the same bank, different groups might be using different ways to value options. Isn’t it strange that we do not have any sensible valuation method for one of the oldest trading instruments?

• Managing Risk

  • This book was published in 2004 and the author criticizes VAR at length. Somehow no one paid heed to Mandelbrot’s warning. The author is somewhat pleased that Extreme value theory is being used by some people for risk management. However he says that Long memory behavior is not being incorporated in to such theories.

By the end of this book, a reader is thoroughly exposed to the key themes of the book : scaling, power laws, fractality and multifractality.

Takeaway:

Most of the financial models taught in universities world over, are “mild-randomness” types. Most of the academic research is concentrated on developing “fixes” to mild-randomness models. However the markets are driven by “wild-randomness”. As long as portfolio managers, traders and quants use “mild-randomness” models, catastrophic losses are inevitable. The book says there are just about 100 odd Fractalists throughout the world who have realized the futility of the current models, have abandoned them for good and are using fractals in their work. For anyone wanting to look at the financial world with fresh eyes, this book is a must read.