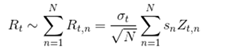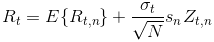Intraday periodicity and volatility persistence in financial markets
The paper titled, “Intraday periodicity and volatility persistence in financial markets”, by Andersen and Bollerslev is a 44 page analysis on volatility modeling and has close to 75 references. This paper is one of the widely quoted papers on intraday volatility modeling. In this post, I will give a brief summary of the main sections of the paper.
Introduction
Return volatility varies systematically over the trading day and this pattern is highly correlated with the intraday variation of trading volume and bid-ask patterns. The authors of the paper conjecture that intraday return dynamics is neglected primarily because the standard time series models of volatility have proven inadequate when applied to high frequency returns data. The paper demonstrates that the difficulties encountered by standard volatility models arise largely from the systematic patterns of average volatility across the trading day and explains a method to estimate and extract the intraday periodic component of return volatility. The datasets used by the authors pertain to intraday data and interdaily data for two assets, one from forex OTC market and the other a futures equity index contract. Most of the models used for volatility modeling on the intraday appear puzzling and in stark contrast to the aggregation studies. One does not find any relationship amongst the parameters of models build at different scales. The authors remark that
Theoretical predictions about the relationship between parameter estimates at different sampling frequencies do not generally apply in the face of strong intraday periodicity, a fact that has gone largely unnoticed.
This paper proposes a generic approach to modeling the intraday pattern and there is no explicit attempt to correct low frequency periodicity patterns
Intraday returns periodicity
The datasets used in the paper is the 5 min returns of DM-Dollar rate over 1 year period and 3 year S&P 500 5 min returns. Also daily returns for DM-Dollar, S&P returns are used to check the analysis at different scales. The authors find that intraday currency returns have almost zero mean as compared to the standard deviation of the returns. Significant deviations from normality is seen via skewness and kurtosis estimates. Also there is a bid-ask bounce effect seen in the data where the returns have a small negative first order autocorrelation. This provides support for the hypothesis that forex dealers position their quotes asymmetrically relative to the perceived true market price as a way to manage their inventory positions, thus causing the midpoint of the quoted prices to move around in a fashion similar to the bid-ask bounce.
The average returns plot show no specific pattern whereas the absolute return plots show the U effect that is often cited in various papers. For both the assets, the systematic return effects are dwarfed by the systematic movements in the return volatility. Several recent studies have attempted to rationalize the U-shape pattern in intraday stock market volatility by strategic interaction of traders around market openings and closures.
Characterization and modeling of the correlation structure in intraday returns
Why is the approach of directly applying ARCH family models on intraday data faulty ? Standard ARCH models imply a geometric decay in the return autocorrelation structure and simply cannot accommodate strong regular cyclical patterns. The authors introduce a stylized model that provides a specification for the interaction between the two components, i.e. intraday periodicity and daily conditional heteroskedasticity.
Here R_t denotes the daily continuously compounded returns calculated from the N uncorrelated intraday return components R_{t,n}. The conditional volatility factor for day t is denoted by sigma_t, while s_n refers to a deterministic intraday periodic periodic component and Z_{t,n} is an IID mean zero and unit variance process. The authors calculate correlation of absolute returns at various scales and observe that the presence of periodic components reduces the overall level of the interdaily return autocorrelations. In contrast, the periodicity may have a strong impact on the autocorrelation for the absolute returns. Even through they find a large positive autocorrelation at a daily frequency, the periodicity has a profound impact on the structure on intraday return dynamics. Based on the correlations and the observed patterns, the authors justify that the stylized model incorporates the conditional heteroskedasticity at the daily level and the strong periodicity at the intraday level.
Implications for Volatility modeling and high frequency return aggregation
This section investigates the question of whether more formal time series modeling of return volatility is impacted by the presence of periodic features at the intraday level. The most common MA(1)-GARCH(1,1) model is fit to a range of time scales for both the currency and the stock futures data. The results show that a variety of theoretical properties for GARCH(1,1) model break down at the intraday level which makes one suspect model misspecification. The following are some of the statistics used to show that standard time series modeling for intraday level is misspecified
-
Variance ration test for absolute returns
-
Half life for the variance in the GARCH(1,1) model
-
Median lag
-
Mean lag
-
Relationship between GARCH parameters at various time scales
The dynamics of filtered and standardized intraday returns
The following decomposition is used to model the deterministic seasonality:
The author use Fourier Flexiblefunctional form to estimate the seasonality factors. The seasonal factor, thus obtained is removes from the return series and the filtered series are modeled via GARCH(1,1) process. The findings show that the filtered series follows GARCH(1,1) closely and the standardized residuals seem to behave in a tamed manner. The same type of observation is made on equity returns data too. The paper thus demonstrates that a simple model can capture intraday periodicity and condition al heteroskedasticity that is exhibited in the intraday volatility patterns.
The classic model that one uses for modeling volatility is MA(1) + GARCH(1,1). However a direct application of this model to intraday data leads to model misspecification. This misspecification arises from the intermixing of intraday patterns with heteroskedastic patterns in the volatility. This paper uses foreign exchange data and equity data to show that there is indeed a misspecification by the direct application of ARCH family. A stylized model is then introduced to get a grip on periodicity. The seasonality functions are estimating via Fourier Flexible form. Once the seasonality is estimated, the return series are deseasonalized and the usual MA(1)+ GARCH(1,1) model is used for volatility modeling.