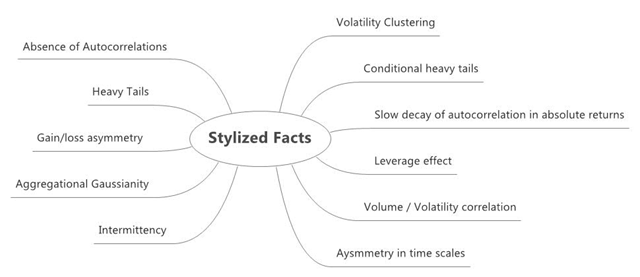
Stylized Facts
The paper titled, “Empirical properties of asset returns: stylized facts and statistical issues”, by Rama Cont presents 11 stylized facts applicable to wide set of assets that should be always in a quant’s working memory. These stylized facts should shape one’s thinking in building financial models.
Stylized facts are the statistical properties of asset prices that are common across a wide range of instruments, markets and time periods. They are usually formulated in terms of qualitative properties of asset returns and may not be precise enough to distinguish among different parametric models. Nonetheless, these stylized facts are so constraining that it is not easy to exhibit even an adhoc stochastic process which possesses the same set of properties and one has to go to great lengths to reproduce them with a model.
Here is a visual that lists the 11 categories under which facts are listed :
The paper also mentions several empirical results. I am listing down a few of them here.
-
Tail properties
-
Returns distribution tends to be non-Gaussian, sharp peaked and heavy tailed
-
The features exhibited are not sufficient for identifying the distribution of returns and leave a considerable margin for the choice of distribution
-
For a parametric model to successfully reproduce the empirical features of the marginal distribution, it must have at least four parameters : location, scale, decay of the tails and eventually an asymmetric parameter allowing the left and right tails to have different behaviors.
-
Mandelbrot’s method can be used to measure the tail index of the distribution
-
Fourth or higher order moments are not numerically stable.
-
Most of the results in the financial literature report the tail index between 2 and 5.
-
Dependence properties of returns
-
Traditional tools of signal processing that are based on second-order properties in the time domain – autocovariance analysis, ARMA modeling – or in the spectral domain – Fourier analysis, linear filtering – cannot distinguish between asset returns and white noise.
-
Absolute or squared returns exhibit significant positive autocorrelation or persistence
-
Definition of volatility is model dependent and volatility correlations are not observable as such, whereas the correlations of absolute returns are computable
-
ACF of heavy-tailed nonlinear time series can have non-standard statistical properties which invalidate many econometric testing procedures used for detecting or measuring dependence.
-
In order for autocorrelations of squared returns to be well defines, one needs finiteness of fourth moments of returns. On the other hand, statistical analysis of returns indicates that the tail index obtained for most assets is typically close to four which means the fourth moment is not a well defined numerically stable quantity.
-
ACF of the squared returns in GARCH(1,1) models can have non-standard sample properties and can generate large confidence bands, which raises serious questions about the methods used to fit these models to empirical data
-
Cross asset correlations
-
PCA bases analysis shows that except the highest eigen value eigen vector, the rest of the eigen vectors and values do not contain any information
-
It is possible to have extremal correlations while their covariance is zero
The paper lists about 114 references! while making various points about stylized facts and statistical properties of assets.