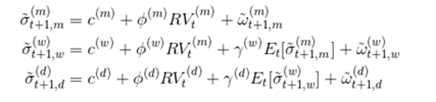A Simple Long Memory Model of Realized Volatility
The paper titled, “A Simple Long Memory Model of Realized Volatility”, is one of the most cited papers in the area of long memory volatility models.
One typically assumes that log prices follow an arithmetic random walk. In this kind of set up, it has been shown in the previous research that integrated volatility of Brownian motion can be approximated to any arbitrary precision using the sum of intraday squared returns. In fact this statement is applicable at a more general class of stochastic processes – finite mean semi martingales (includes Ito processes, pure jump processes, jump diffusion processes). Sum of intraday squared returns, ``Realized volatility, is a nonparametric measure that asymptotically converges to the integrated volatility as the sampling frequency increases. The flip side to this utopian scenario is the microstructure noise that one needs to contend with as the time scales become finer. Noise introduces a significant bias in the RV estimate. Hence one has to make a tradeoff between measurement noise and unbiasedness. In many papers, researchers have used anywhere between 15 min to 30 min intervals, as they might have observed that as the shortest return interval at which the resulting volatility is still not biased. Another approach that can be adopted to deal with the microstructure noise is to filter away the noise using the autocovariance structure of k tick aggregated returns. Well one might have to search a grid to get an optimal k to begin with. In an earlier paper by Corsi, one such filtering method is described.
The author uses 12 years of FX tick data and finds the following four patterns throughout:
-
Fat tails
-
Long memory in volatility, i.e. autocorrelation of the squared returns and absolute returns show very strong persistence which lasts for long time interval. In the case of dataset analyzed in the paper, the persistence lasted for 6 months
-
Log realized volatility was more close to normal distribution
-
Presence of scaling and multiscaling behavior
Why another volatility model? Is GARCH(1,1), the emblematic volatility model not enough ? Can’t we us some variant of GARCH family?
-
GARCH(1,1) models suffer from one weakness, i.e. their autocorrelation structure is exponential and not hyperbolic. Hence the persistence patterns die off very soon. Also there is a stringent tradeoff between the possibility of having a sharp changes in the short term volatility and the ability to capture long memory behavior of volatility
-
One way to introduce long memory is via Fractionally integrated GARCH, FIGARCH. However the author is of the view that the joint estimation of parameters is a very difficult problem. Also heuristic methods of estimating the differencing parameter is known be biased and inefficient
-
All the GARCH models can manage is unifractal patterns and not multifractal pattern
The obvious question is what does it take to build a model that has the characteristics of multifractal behavior + long memory+ fat tails ? The strict answer to this comes from physicists who are of the view that only multiplicative processes lead to multifractal processes. Any multiplicative process will be difficult to identify and estimate. What’s the way out? The author takes a view that the long memory and the multiscaling features observed in the data could also be only an apparent behavior generated from a process which is not really long memory or multiscaling. This is what motivated him to come up with an additive model that captures the stylized facts present in the dataset.
What’s the basic idea behind the model introduced in the paper?
The author banks on “Heterogeneous Market Hypothesis” that says that the presence of market increases volatility. In a market where there are homogenous agents, a bigger set of agents should make the prices converge at some mean price. Reality is something else. The bigger the market size, the more correlated is volatility. One can think of markets populated with three kinds of agents, intraday agent, mid frequency trading agent and low frequency trading agent. This means that a volatility model needs to take in to consideration at at least three time scales. HARCH process is one that incorporates this kind of a behavior. It belongs to the wide ARCH family but differs from other ARCH-type processes in the unique property of considering squared returns aggregated over different intervals. One stylized fact that HARCH shows is that longer time interval volatility has an influence on shorter time intervals. The paper builds up on HARCH model and introduces a cascade of model between the three time scales: daily, weekly and monthly volatility processes. There is one equation for each time scale and three equations are related in a way that monthly volatility feeds in to weekly volatility which in turn feeds in to daily volatility.
The economic interpretation is that each volatility component in the cascade corresponds to a market component which forms expectation for the next period volatility based on the observation of the current realized volatility and on the expectation for the longer horizon volatility. The daily volatility equation can be seen as a three factor stochastic volatility model where the factors are directly the past realized volatilities viewed at different frequency.
The author then hypothesizes that the RV computed on the filtered returns on a daily basis can act as a proxy for the LHS in the above equation. This turns the entire equation in to a simple time series representation of the cascade model that becomes easy to estimate. The author terms that above model as HAR-RV, Heterogeneous Autoregressive model for the realized volatility. The authors simulate paths from the above model and show that the behavior matches the observed data in the following aspects
-
Visual inspection of daily return series and daily RV series
-
PDF of returns for different time horizons
-
Persistence of autocorrelation for daily RV
-
Behavior of partial autocorrelation coefficients for daily RV
-
Scaling behavior
The authors use standard OLS method with Newey-West covariance correction for estimating the model parameters. A comparative study of performance against a set of standard volatility models shows that HAR-RV manages give a reasonably good out of sample forecasting performance. Simplicity of its structure and estimation is definitely an appealing aspect of HAR-RV model.