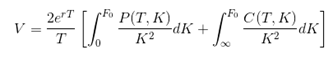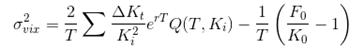What’s wrong with VIX
The paper titled, “Extracting Model-Free Volatility from Option Prices: An Examination of the VIX Index”, is a very interesting paper that talks about the problems in the VIX index computation that is currently being used at CBOE. Other stock exchanges throughout the world are also following a similar method for disseminating VIX, called the fear index. One of the most interesting conclusions of the paper is this :
VIX underestimates the true volatility in times of panic, i.e. when we need the fear index the most, it acts as an imprecise gauge
Before 2003, VIX was computed by averaging the ATM volatilities. The volatilities were in turn inferred from the option prices via Black Scholes model. Post 2003, VIX index computations was changed to reflect a methodology based on the fair value of a variance swap. The valuation of variance swap is via replicating argument and hence is not dependent on a specific model. Well, the previous statements is not entirely correct. The stock is assumed to be GBM with constant diffusion parameter, instead of let’s a jump diffusion model. It is “model free” in the sense that it is using the actual option prices quoted in the market to obtain VIX. However as far as using the replicating argument is concerned, a model is used after all to compute the risk neutral expectation of realized volatility. In any case, CBOE had to put in some tweaks in order to use the theoretical fair price of variance swap in the real world that has finite strike range and discrete strike interval.
Why should be there any error at all ?
The fair value of future variance is based on the replicating argument and it is given by the following formula :
In the real world, continuous strikes are not available nor are strikes available from 0 to infinity. So, there is bound to be some approximation error between the theoretical fair value and its real world implementation. In CBOE implementation the VIX is computed by the following formula :
where F0 is the forward index level, T is the option maturity, Ki is the strike price of ith OTM option, K0 is the first strike price below F0, Q(T,Ki) is the midpoint of the latest available bid and ask prices for the option, r is the risk free rate and Delta Ki is the strike price increment. An adjustment at the strike price K0 is made by redefining
Q(T,K) as the average price of call and put options.
What are the types of errors that occur in the current VIX avatar ?
The paper mentions four types of approximation errors :
-
Truncation error : By default there are only finite number of strikes and hence it is a finite interval over which the integration is carried out.
-
Discretization error : The strikes are not continuous on the real line and hence the integral has to be discretized
-
log expansion error : Instead of the log function in the fair value of the variance swap, a Taylor series expansion is used and this gives rise to approximation error
-
Interpolation error : The variance over the next 30 days is computed by a linear interpolation of variance at two different maturities. There can be a problem if the variance is a nonlinear function of maturity
How large are these approximation errors ?
The authors simulate option prices using a price process that has a stochastic volatility component and random jumps. Since the simulation starts off with a known volatility smile, it is easy to check whether VIX is giving the right estimate or not. The authors analyze only the first three of the above approximation errors. Option prices at various strike ranges with different strike price intervals and varying maturities are simulated. CBOE VIX is computed for all the simulated prices and a thorough error analysis is done in the paper. Here are the findings :
-
Truncation error : The integral in the fair value of the variance swap is truncated and this gives rise to an underestimation of the true variance
-
The truncation errors are generally negative and can be as large as 15% of the true volatility
-
Truncation errors are negligible if the truncation points are at least 3 standard deviations from the initial asset price
-
When volatility rise, then a large part of approximation error is the truncation error. VIX is actually very imprecise in the times of crisis, i.e. times when it is most needed
-
Truncation error increases when interval of truncation is asymmetric( intervals are asymmetric in the real word)
-
-
Discretization error : This arises mainly because of the integral is numerically evaluated. The discretization gives rise to an overestimation of true variance
-
The numerical integration requires integrating a function that has a kink. Any approximation of this integral will give rise to an error. Besides this the CBOE averages the option prices near the kink
-
Discretization errors are generally positive and can be as large as 6.3% of the true volatility
-
Discretization errors are negligible when the strike price increment is less than 0.5 standard deviation of the underlying asset
-
-
log expansion error : This error is a negligible percentage of total approximation error
How to fix these errors ?
The authors propose a natural cubic spline interpolation of the implied volatility curve within the available finite strike range and extrapolate the smoothed IV curve outside the finite interval based on the slop of the curve at the end points. What ’s the advantage of this interpolation ? For one, you can use a finite grid to integrate various terms. Secondly, the extrapolation can reduce the truncation error. With this simple solution, discretization and truncation errors can be significantly reduced. As a robustness check, the authors use smoothing method to test the model prices generated by a stochastic volatility with random jumps model. They find that the smoothing method is consistent across all volatility and index levels. The maximum error via smoothing fix is only about 8 index basis points whereas the CBOE VIX errors range between +79 and –198 index basis points.
CBOE procedure for computing VIX leads to positive discretization error and negative truncation errors. At modest levels of volatility, they appear to mostly offset each other. At lower volatility levels, the discretization error dominates and hence there is an over estimation of true volatility. At higher volatility levels, the truncation error dominates and hence results in an underestimation of true volatility. A simple fix suggested in the paper is natural cubic spline plus extrapolation that smoothens the IV curve and thus reduces the discretization error and the truncation error.