Probability Through Problems

This book has a nice collection of problems related to Modern Probability. Unlike the classical problems which are related to discrete variables, the problems in the book are related to variables whose measure is a combination of discrete , absolute continuous and singular measures.

My motivation in going through this book was Chapter 10 which is on Conditional Expectation. Martingales are very important mathematical objects , as far as math-fin stuff is concerned. They appear everywhere, be it option pricing/ hedging/ stat arb etc.They also play an important part in stochastic portfolio theory. Martingales are Conditional Expectation variables.

Conditional expectation is a very tricky concept to understand mainly because there is no ready formula to compute Conditional Expectation. You can only guess the form based on a few constraints. E(X/Y) is easy to compute if Y is an event or if Y is a discrete variable. However it becomes a non trivial problem if Y is a general random variable. Existence of such a variable is guaranteed by Radon Nikodym derivative.  Computation though is from indirect means.

If you look at the definition of Conditional Expectation , it goes something like this :

Let X and Y be any random variables. The conditional expectation  E[ X / Y ]  of X given Y is a random variable such that

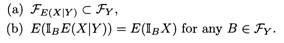
Each of the above statements need to be understood carefully. The first statement says that Sigma algebra of this variable is always a subset of Sigma algebra generated by Y. Second is a condition on projection operator, ( projection of X on the sigma algebra generated by Y).

Now one way to understand these issues is to actually pick up a few random variables and calculate Sigma algebra and see to it the above two conditions do actually satisfy. Another way is to look up books like these where exercises are tailor made so that one can understand these aspects. In that aspect, the problems in Chapter 10 are priceless as they give clues to compute implicitly the conditional expectation of general random variables.

  Takeaway:

Conditional Expectation and the relevance of Radon-Nikodym derivative is shown via a superb set of problems. The fundas relating to  Conditioning a variable on a sub sigma algebra become crystal clear after working through these problems.