Finite Markov Chains : Summary

This book is an awesome resource for understanding finite Markov chains. The book is written in Pre-Latex era and hence one has to struggle to follow the notation. Is the Struggle worth it? IT IS, if you are looking at developing a Matrix perspective towards “Discrete Stochastic Process”. IT IS NOT, if you are looking at quick and dirty formulae. The first version of the book appeared in 1960 and second version in 1976. I wasn’t even born when these books came out –:) . However like many things in life, things that age have their own charm. The book serves as a precursor to understanding Markov chain Monte Carlo method which is an essential tool for any quant.

**Chapter 1: Pre-requisites:
**Most of the stuff can be quick read in this chapter. What I found interesting was the mention of set theory concepts such as equivalence relation, weak ordering relation, minimal elements etc. One must patiently go over these stuff as they find immense application in classifying Markov chains. An attempt is made to describe a simple stochastic process and readers might find this example appealing before venturing in to complicated stochastic processes. I understood Cesaro-Summability and Euler Summability clearly in this context , even though I had quick read them in “Understanding Analysis”- Abbott.

Chapter 2: Basic Concepts of Markov Chains

The chapter starts off by defining a Markov process which essentially is a process where essentially previous outcome is all that is needed to predict the probability of future outcome. Markov chain is a finite Markov process where the transition probability from step i to step j does not depend on the trail number. One of the equivalent ways to state a Markov chain is that , given the present, the past and future are completely independent of each other. To deviate in to philosophy here a bit, I think we should lead our lives also like a Markov process. Whatever be the past, given the present, we must work in the present, be in the NOW so that future becomes independent of the past. Ok, enough of this philosophy crap J , Let me get back to the contents of the chapter.

What’s the difference between Markov Process and Markov Chain ?

Well, Markov chain is a type of Markov process. Apart from that, one of the biggest differences arises from the fact that a Reverse Markov process is also Markov process but a reverse Markov chain need not be a Markov chain. The transition probability matrix of a reversed Markov chain may well depend on the trail number and hence does not qualify to be a Markov chain. This nifty difference is sometimes not highlighted clearly most of the times in other books.

The author gives a set of examples representing Markov chains to get an idea of various finite Markov chains one can come across. One of the reasons I got interested in Markov chains is that they are an excellent computational tool for classic probability problems. At the same time, they serve as an ideal platform to understand stochastic processes. I used to struggle to work with problems involving absorbing barriers, reflecting barriers in a simple random walk. Setting up a recurrence relation and solving using PDE approach or some tricky method never gave me a tool to understand the stuff. Markov chains on the other hand actually give a fantastic way to compute these using matrices. I love when any problem is formulated using matrices. It makes everything so pleasant for a problem solver.

Classification of states in a Markov Chain:

The author uses set theory concepts such as partial ordering, equivalence classes induced by partial ordering, minimal elements of the partial ordering of equivalence classes etc to classify the states of a Markov Chain. Well, I was aware that “Relation” can be used to define equivalence classes that partition a set. But beyond that, my understanding of “Partial Ordering”, “Minimal Elements” etc was shallow. Hence I took a detour for a few hours and went through “Naive Set Theory” – Paul Halmos. I managed just enough to understand stuff about Markov Chain.

You start off with a relation – iRj, you can reach state i from state j, meaning it is a type of relation and you can then extend this to another relation ( iRj and jRi ) meaning you can reach i from j and j from i . So, you start with a weak ordering relation, and extend it form equivalence classes. When I first came across these concepts, I found some resistance in understanding these ideas. Why should I care if you start with a weak relation and you can extend that weak relation so that you can form equivalence classes?

Well, all these concepts make tremendous sense when you look at a Markov Chain. Firstly,the weak ordering relation can be extended to”communication” relation to first classify the states in to equivalence classes. Subsequently, you can order these states and the minimal elements of these ordered states form ergodic states. Cutting the fancy stuff around the word ,”minimal”, all it means is that if you take any element x of a set U, if iRx holds then xRi holds too. All those elements i form an ergodic set. One must understand the reason for this ordering and the rationale behind ordering. Once you order stuff , you have the transition matrix as follows

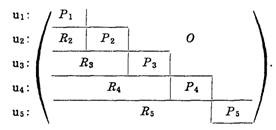
This pattern emerges once you order the states accordingly. The first thing that strikes you about the above matrix is that you can higher powers of this matrix retains the individual transition matrices on the diagonal and thus one can individually analyze these matrices without worrying about the entire chain.

The chapter then goes in to giving labels to various kinds of Finite Markov Chains. There are two broad categories of Markov Chain. Firstly the chains which do not have transition states. Secondly, the states have transition states.

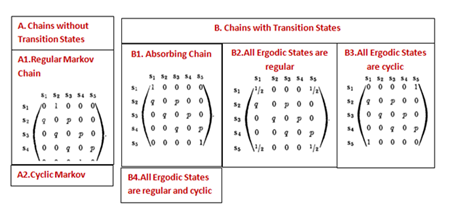
Chains without Transition States are also called chains with single ergodic set (ergodic chain). They can be further divided in to:

• Regular Markov chains symbolize the transition matrix where each state can be reached from any other state. Thus all the elements of the transition matrix will eventually become positive.

• If the chain has a period d then such a chain is called cyclic Markov chain.

Chains with transition states can be further divided in to

• Absorbing chain where the ergodic states are unit sets

• All ergodic sets are regular. This means if you take an ergodic set, then you can reach any state from any state in that ergodic set

• All ergodic sets are cyclic. This means that the states in the ergodic state are cyclical

• Both cyclical and regular ergodic states

As can be seen from the above illustration, almost all the categories can be expressed using simple random walk. Given various states, what are the kinds of questions that one would be interested in?

Regular Markov Chain Questions

• If a chain starts in Si, what is the probability after n steps that it will be in Sj?

• Can we predict the average number of steps that the process will be in Sj? Does it depend on where the process starts?

• We may wish to consider the process as it goes from Si to Sj. What is the mean and variance of the number of states passed? What is the probability that process passes through Sk?

• Study a subset of states and observe the process only when it is in these states

Transient States Questions

• Probability of entering a given ergodic set , starting from Si

• Mean and Variance of the number of times that the process is in Si, before entering an ergodic set, and how this number depends on the starting position ?

• Mean and variance of the number of steps needed before entering an ergodic set starting at Si?

• The mean number of states passed before entering an ergodic set , starting at Si

The book is sequenced in a way that the above questions are answered systematically. Absorbing Chains, Regular Markov Chains and Ergodic Chains are covered as specific chapters.

Chapter 3: Absorbing Markov Chains

The book looks at Absorbing Markov chain by segregating transient states from Persistent states. It then analyzes Transient State matrix and derives basic formulae in terms of matrix operations. The highlight of this book is “Fundamental Matrix Approach”. For any Markov chain, the book tries to zero on to a specific matrix which is fundamental to all the calculations relating to the Markov chain

Fundamental Matrix for Absorbing Markov Chains is derived: 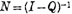. The reason it is called Fundamental is because it is used in formulating solutions for most of the interesting questions about Absorbing Markov Chains

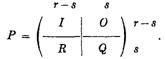
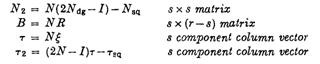
Solutions in Matrix form are furnished for the following:

• Total # of times that it is in various states

• Probability of absorption

• Total time before it gets absorbed

• Variance of total time before it gets absorbed.

From the examples give, all of them have high variance for the mean estimates. Is this a general case ? I mean are all the estimates of Markov chain characterized by high variance? I don’t know. Will find out someday.

Chapter 4: Regular Markov Chains

Regular Markov Chains are explored in this chapter using Matrices. The limiting properties of Regular Markov chain are explored where the chain settles down in to a constant row matrix after n iterations. This limiting markov chain is then used to state “Law of Large Numbers” . Most of us would have heard of “Law of Large Numbers” for independent trials where the statements become weak law or strong law based on whether the convergence is almost sure or convergence is in probability. This law from a Markov chain is radically different as it removes , “iid” clause from the law of large numbers and thus massively expanding its scope. This form of law was worked out by A.A.Markov in 1907. In the 100 odd years that have passed since then, Markov chains are now practically used in tons of applications.

• The book’s USP is Fundamental Matrix and hence one sees the Fundamental Matrix derived for these Regular Markov chains as well, which takes the form 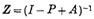. This matrix is then used to compute

• Mean of first passage times for various states

• Variance of first passage times for various states

• Correlation for the above events

The chapter then talks about Central Limit theorems for Markov chains. It merely states the theorem and defers proving the same. CLT for Markov chains connects the (average number of visits to a particular state, its limiting value) WITH Standard Normal Distribution.

The preface in the book mentions one of the reasons for the second edition. In the above formulae, Fixed weight vector was used to obtain the Fundamental Matrix. However there is an alternative method where any constant row vector can be used to obtain Z. The appendix of the book mentions the paper where pseudo-inverses are used. 

Chapter 5: Ergodic Markov Chains

What if there is cyclicality in chains with transient states ? This chapter delves in to the math behind such chains. Condition for a markov chain to be considered as reversible is also mentioned. A Markov chain being reversible or not, has a great impact from a simulation perspective.The book then talks about further extensions to the above mentioned chains. Basically it involves stuff where a transient chain is made in to an persistent chain forcefully to compute some interesting stuff and vice versa.

In the concluding chapter, the book shows various application of Markov chains like

• Random walks

• Ehrenfest Model

• Application to Genetics

• Learning Theory

• Mobility Theory

• Open Leontif Model

By no means these examples should make you think that Markov chain is used as Toy examples. The research and amount of stuff that has been done on Markov chains for the last 100 years is so massive that it has found applications in a wide variety of fields from sports betting to

Take away:

Persi Diaconis (the iconoclastic Stanford Professor) remarks “To someone working in my part of the world, asking about applications of Markov chain Monte Carlo (MCMC) is a little like asking about applications of the quadratic formula. The results are really used in every aspect of scientific inquiry.”

Indeed, Markov Chain Monte Carlo methods have revolutionized the field of statistics. My takeaway from the book is not so much so about simulation as it is about understanding Martingale Objects. While formulating a Martingale, If you are able to visualize vaguely the discreet Markov Chain in the background, I bet your understanding will be much better.