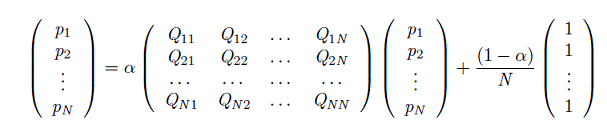I am hooked on to “Markov Chains” these days and they seem to fascinate me as the applications are in almost every field that I look at. I happened to go over Page Rank algo. From a Markov chain’s perspective, the algo can be summarized  in 2 steps

Step 1 : Represent a random surfer’s movement as a Markov chain

clip_image002

Here N is the total number of pages indexed by Google, Q is a transition matrix( irreducible, a periodic) that captures the transition probability of moving from one page to another , p is the page rank of the pages on the internet and alpha is adjustment factor to take in to consideration the inherent importance of a page.

Step 2 : Solve the Markov chain equation of Step 1 to compute the page rank. This is solved using iterative methods from Linear algebra (SVD)

This algo needs to be tweaked day in day out as the transition probability matrix keeps changing every second. As soon as any webpage (i) puts out an external link to any of the page (j), the probability corresponding to the origin and destination page Qij in the transition matrix changes.

Combine these 2 steps with more than a decade of computational learning about each element in the transition matrix , and you get a multi-billion dollar company called “Google” Surprised smile