Linear Models with R : Summary

[

The book is written by Julian Faraway , a Statistics Professor at University of Bath.  The book seems to be culmination of lecture notes that the professor might have used over the years for teaching linear models. Whatever be the case, the book is wonderfully organized.  If you already know the math behind linear models, the book does exactly as it promises in the title,i.e, it equips the reader to do linear modeling in R.

Let me attempt to summarize the book:

Chapter -1 Introduction

The chapter starts off with emphasizing the importance of formulating any problem. Formulating the problem in to statistical terms is the key aspect in any data analysis or modeling exercise. Once you formulate the problem, answering it is mostly a matter of mathematical or experimental skill. In that context, Data cleaning is THE most important activity in modeling. In formulating the problem, it is always better to understand each predictor variable thoroughly. The author talks about some basic data description tools available in R. He also mentions Kernel density estimation as one of the tools. I was happy to see a reference to one of my favorite books on smoothing, a book by Simonoff in the context of KDE. The chapter talks about the basic types of models that are covered in various chapters, i.e Simple regression, Multiple regression, ANOVA, ANCOVA.

Chapter – 2 Estimation

The chapter defines a linear model, i.e. parameters enter linearly, the independent terms can be present in any non linear way. Predictors need not be linear is the basic takeaway. The geometric representation of linear model framework is illustrated below:

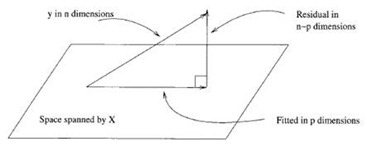
It is clear from the above visual that regression involves projection on to the column space of the predictor space. If it is a good fit, the length of the residual vector should be less. To be precise, Linear Regression partitions the response in to systematic and random part. Systematic part is the projection of Y on to subspace spanned by the design matrix X. The least square formulae are quickly derived, i.e beta estimate and its variance, fitted values and their variance, estimate of error variance. Estimate of residual variance is a formula that depends on Residual sum of squares and residual degrees of freedom. To derive this little formula, one needs to know the connection between trace of the matrix and expected value of a quadratic form. There is a section on Gauss Markov theorem that basically states that linear regression estimate of Beta is Best Linear Unbiased Estimate. Least squares framework also matches MLE estimate if the error are assumed to be iid.

There is also a subtle point mentioned that is missed by many newbies to regression, i.e. Coefficient of determination / R squared has an obvious problem when the linear model has no intercept. The intuition behind R squared ( 1- RSS/TSS) is : Suppose you want to predict Y. If you do not know X, then your best prediction is mean(Y) , but the variability in this prediction is high. If you do know X, then your prediction will be given by the regression fit. This prediction will be less variable provided there is some relationship between X and Y. R squared is one minus the ratio of the sum of squares for these two predictions. Thus for perfect prediction the ratio will be zero and R squared will be one. However this specific formula is meaningless if there is no intercept in the model.

The chapter then talks about Identifiability in a model that typically arises when the model matrix is not full rank and hence not invertible.One way to check for identifiability problem is to compute eigen values of the design matrix. If any of the eigen values is close to 0 or 0 , then you have a problem of identifiability and hence the problem of collinearity. Clear lack of indentifiability is good as software throws up error or clear warnings. But if there is a situation which is close to unidentifiability, then it is a different problem where it is the responsibility of the analyst to interpret the standard errors of the model, and take a call on the variables  that have to be filtered away or dropped.

The best thing about this chapter is that it shows what exactly happens behind lm. I remember a conversation I had with my friend years ago about an interview question. My friend was mentioning about this favorite question that he always used to ask in interviews, while recruiting fresh graduates: “ Here is a dependent variable Z taking 3 values z1,z2,z3,z4. Here are two independent variables X and Y taking values (x1,x2,x3,x4) and (y1,y2,y3,y4). If you fit a linear model , give me the estimate of predictor coefficients and their variance?. “ Starting from a very basic values for which the linear model works well, he used to progressively raise the bar with different values of Z,X,Y. For people who are used to software tools doing the computation, such questions are challenging. Well, one does not need to remember stuff, is the usual response. Ok..But there is always an edge for a person who knows what goes on behind the tools. This chapter in that sense is valuable as it actually shows the calculation of various estimates, their variances using plain simple operations and then matches these values to what lm() throws as output. I guess one simple test whether you know linear regression well is as follows:

• lm(y~x,data) throws the following output :

  • [coefficients ,residuals, effects ,rank , fitted.values, assign, qr, df.residual, xlevels, call, terms, model ].

  • Can you manually compute each of the above output using plain simple matrix operations and arithmetic operations in R?

• summary(lm(y~x, data)) throws the following output :

  • [call, terms, residuals, coefficients, aliased, sigma, df, r.squared, adj.r.squared, fstatistic, cov.unscaled]

  • Can you manually compute each of the above output using plain simple matrix operations and arithmetic operations in R?

Well, one can obviously shrug the above question as useless. Why do I need to know anything when lm() gives everything. Well it depends on your curiosity to know things. That’s all I can say.

**
Chapter – 3 Inference**

The chapter starts off with an important framework for testing models, i.e. splitting sum of squares of a full model in to orthogonal components. Let me attempt to verbalize the framework. Lets say you come up with some reduced model and you want to check whether the reduced model is better than the full model. The residual of the large model is compared with the residual of the small model. If the difference between the two models is less, then reduced model is preferred. Now to standardize this number, it is divided by residual for the large model.

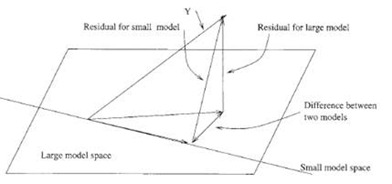
If this ratio is small, then there is a case for reduced model. This ratio, RSS_red – RSS_full / RSS_full (need to adjust for degrees of freedom) is the same test statistic that arises out of likelihood-ratio testing framework. The best thing about this framework is that you don’t need to remember any crazy formulae for various situations. If you get the intuition behind the framework, then you can apply to any situation. For example if you want to test that all the coefficients are 0, i.e reduced model contains only intercept term , then all you have to do is calculated (RSS_Null – RSS_Model)/(p-1) / ( RSS_Model/n-p) , compare it with F critical value. If it is greater than F critical, you reject the null and go with the model. Infact this output is given as a part of summary(fit) in R. The good thing about this framework is that you can test the significance of a single predictor using this framework. Reduced model would be full model minus the specific predictor. This is compared to the Full model and the computed F value can be used to judge the statistical significance of the predictor. The chapter mentions  I() and offset() functions in the context of testing specific hypothesis in R.

The chapter then talks about forming confidence bands for various predictor betas in the regression framework. The good thing about this text is that it shows how to compute them from scratch. So once you know those fundas, you will not hesitate to use functions like confint in R. Blindly using confint would be difficult, atleast for me.

Obviously once you have the model, the confidence interval for each of the parameters in the model, the next thing you would be interested is prediction. There are two kinds of prediction and one needs to go over this stuff to understand the subtle difference. In R, you can use predict function with the argument “confidence” to predict the mean of response variable given a specific value of the independent variable. You can use predict with the argument “prediction” to predict the response variable given a specific value of the independent variable.  There is a subtle distinction that one needs to pay attention to.

There are many problems of applying regression framework to observational data like lurking variable problem, multicollinearity problem. The section makes it extremely clear that non-statistical knowledge is needed to make a model robust. The section also makes the distinction between practical significance and statistical significance

Statistical significance is not equivalent to practical significance. The larger the sample, the smaller your p-values will be, so do not confuse p-values with an important predictor effect. With large datasets it will be very easy to get statistically significant results, but the actual effects may be unimportant.

**
Chapter 4 - Diagnostics**

The chapter starts off by talking about three kinds of problems that might arise in a linear regression framework.

First type of problem arises when the assumption that error term in the model is a iid constant variance model fails. How does one check this after fitting a model ? One way to check this is , draw a fitted vs residuals plot that graphically shows presence of nonstationarity if any. If there is non constancy in the variance, one can look at square root or log or some transformation of the dependent variable so that residuals plot look like random noise. Also a simple qqnorm of the residuals gives an idea of whether the residuals follow a Gaussian distribution or not. Sometimes one tends to use studentized residuals for the normality check calculations. It is always better to check these things visually before doing some statistical test like Shapiro.test etc. The other problem with residuals that can arise is the autocorrelation. One can use Durbin Watson test to test the autocorrelation amongst residuals in a linear model.

Second type of problem arises because of unusual observations in the data. What are these unusual observations ? Any observation that has a great say in the beta values of the model can be termed as unusual observation. One must remember that even though the error term is assumed iid, the variance of fitted values is dependent on hat matrix and error term sigma. So if the values in the hat matrix are high for a specific observation , then the fitted value and observed value be very close and hence might reflect an incorrect fit from an overall data perspective. These points are identified by their “leverage” property. Thus Leverage depends on the spread of the independent variables and not on the dependent variable. In R, the summary of a fitted model gives hat values. One can always use half normal plots to see highly levered observations.

The other type of unusual observations are outliers. The book mentions the use of cross validation principle to diagnose outliers. Well to apply cross validation principle , one needs to actually regress n times ,n being the number of data points. However a nifty calculation shows that a variation on studentized residuals, i.e externally studentized residuals are an equivalent measure to check whether an observation is outlier or not.

An influential point is one whose removal from the dataset would cause a large change in the fit. An influential point may or may not be an outlier and may or may not have large leverage. Cooks distance is used to compute the influence of a specific point on the slope and intercept of the model.

So, all in all it is better to produce 4 visuals in diagnosing a linear regression model, externally studentized residuals, internally studentized residuals, cooks distance and Leverage. Any unusual observations are likely to be identified with these visuals. I think one way to remember these 4 tests is to give it a fancy name, “The Four Horsemen of Linear Model Diagnostics”

The third type of problem arises when the structural equation assumed itself is wrong. The chapter talks about two specific tools to help an analyst in this situation, a) Partial residual plot(better for non linearity detection), b) Added variable plot ( better for outlier / influential obs detection) . The logic behind added variable plot is : Let Xi be the predictor of interest. Regress Y with all other Xs , compute residuals. Regress Xi with other Xs and compute residuals. Plot the two residuals to check influential observations. The logic being Partial residual plot is : Plot a graph between Xi and the residuals contributed by other Xs.prplot in faraway package does this automatically.

One of the best functions that can be used to get all the relevant diagnostic values of a fitted model is ls.diag function. ls.diag function gives hat values, standardized residuals, internally studentized residuals, externally studentized residuals, cooks distance, correlation, scaled covariance, unscaled covariance and dfits values.

Overall , the visuals and statistical tests mentioned in this chapter are very critical in diagnosing the problems in any linear regression model. It is easier to fit any model with powerful packages. However this easiness with which the model is fitted might result in sloppy models. Hence one must atleast perform let’s say half a dozen diagnostic tests on the output of the model and document it along the model results.

**
Chapter 5 - Problems with Predictors:**

The chapter focuses on the problems that might arise with Predictors in a linear regression relation. The first problem is the measurement problem in the independent variable. It is likely that observational data display variation from their true values. The problem with measurement error in the independent variable is that the estimates for such variables are biased downwards. The section introduces a method called Simulation Extrapolation(SIMEX) method to deal with such a situation. The principle is very simple. You add random noise with different values of variance to the independent variable, estimate the coefficient for that independent variable in the regression equation. Subsequently try to estimate the relationship between the coefficient and error variance. It is given a fancy name SIMEX, simulation extrapolation method.

There is a section that talks about changing the scale of the variables so that coefficient are sensible. The basic takeaway from this section is that by scaling, the r square of the model, p value of the anova test remains the same, the scaled variable beta and standard error gets scaled. The final aspect that the chapter talks about is the collinearity. I remember vividly how difficult I felt to understand and explain this aspect to someone who had asked me to verbalize it. It was pretty embarrassing situation for me. Back then, I tried to understand and verbalize conditional number and VIF but couldn’t. Now when I revisit this topic, it all looks pretty straight forward. The estimates for the regression includes an inversion of cross product of design matrix with itself. This inversion exists only if the eigen values are large enough. Why ? Eigen values being large means that there exists a projection on to the subspace spanned by that eigen vectors.So, conditional number is basically a thumb rule that compares the largest eigen value to a specific eigen value and takes a call on whether there is collinearity. The other metric to check collinearity is VIF, variance inflation factor. In simple terms, all you need to do is regress a specific variable in the design matrix with rest of the variables of the design matrix, find the r squared and if its high, then it is likely that there is collinearity. Again straightforward explanation and computation. The R package associated with this book,  “faraway”, has a function vif() that does VIF calculations for all the variables at one go.

Chapter 6 - Problems with Errors

The chapter starts off with a discussion about the possible misspecification of the error model in the linear regression framework. The errors need not be iid but might have a covariance structure amongst them. For such cases, one can use Generalized least squares. Another case is where the errors are independent but not identically distributed. For such cases, Weighted least squares can be used. The chapter talks about both these methods.

For GLS, you start off with a basic estimate of covariance structure, fit a linear model and then recalculate the covariance structure. You do this a number of times till the covariance structure converges. Easier way is to use nlme packages that does this automatically. For WLS, one can use the weights option in the lm function to specify the weights that need to be used for the regression.

The chapter then discusses various methods to test lack of fitness of a model. One obvious way to increase fitness is to fit higher order terms. But this is always associated with higher uncertainty in the estimates. The section discusses a replication type regression check , which in the end , the author himself admits that it might not always be feasible.

The outlier detection using leave-one-out principle might not work in cases where there are many outliers. In such cases when the errors are not normal, robust regression is one of the methods that one can use. The methods covered under robust regression are least absolute deviation regression, Huber’s method, least trimmed squared regression. All these regressions can be done from the functions from MASS package. Robust regression methods give estimates, standard errors only. They do not provide F value and p value for the overall model. Least trimmed squared regression is most appealing as it can filter out higher residual values. The downside to Least trimmed squared regression is the time taken for the regression. So as an alternative the author suggests simulation and bootstrapping methods. The section also gives an example where Least trimmed square method outperforms Huber estimate and normal regression.

Chapter 7 - Transformation

There are ways to transform the predictors or dependent variable so that the error terms are normal. It all depends on whether the error term enters in a multiplicatively or additively. For example a log transformation of the Y variable makes the error enter in a multiplicative manner and hence the interpretation of the beta coefficients are also different. If you fit a linear model, then the coefficients are interpreted as multiplicative in nature and hence for a unit change in predictor, the fitted variable changed in a multiplicative fashion. Log transformation is something that one can check to begin with, as it removes the non linearity in the relationship and makes it a linear relationship. YVonneBishop is credited with the development of Log Linear Models

There is also a popular transform called the Box-Cox transform that applies the best transformation possible so that log likelihood is maximum for the said transformation. There is a function called boxcox in MASS package that automatically does this.Box cox transformation applies a transformation for a specific lambda, so you got to choose the best lambda. Boxcox function in MASS gives a graph between lambda values and their log likelihoods. Looking at the graph, one can choose a specific lambda, apply the transformation and fit a linear model. Besides Box-Cox transformation, there are other types of transformations that one can look at such as logit, Fischer Zs transformation etc.

The chapter has a section on hockey-stick regression where separate lines are fitted for various clusters of data. The way to go about in R is simple. You code two separate functions for these clusters, use in the regular lm framework using I() function.lm() throws out the coefficients of the functions. There is also a section on polynomial regression , orthogonal polynomial regression and response surface model

The last section of this chapter talks about B-splines, an interesting way to build smoothness and local effects in to regression model. In the previous section, hockey-stick regression was used to cater to local clusters/local behavior. Polynomial regression was used to make the regression fit smooth. However the problem with polynomial regression is that it does not take local behavior in to account and the problem with hockey stick regression is that it is not smooth(discontinuous straight lines basically). A good mix of both features , i.e. smoothing and local effect is brought out by B-Splines. The concept is simple. You decide on a certain knots, fit a cubic polynomial between the knots and join them.

The chapter ends with a reference to a non parametric model , whose form is follows :

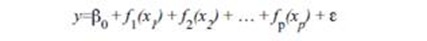
I think locfit is a good package that can be used to obtain the above non parametric model. Clive Loader has written a fantastic book on local regression. Will blog about it someday. I am finding it difficult to strike a balance between the books I am yet to read and books I am yet to summarize!. Don’t know how to strike the right balance.

For me, the takeaway from this chapter is the boxcox function available in MASS that one can use to get a sense of suitable transformation. Before applying any transformation , it is advisable to look at at least 4 plots , internal studentized residual plot, external studentized residual plot, hat value plot and cooks distance plot. Because sometimes by removing the unusual observations, you can get a decent linear reg fit with out any transformation whatsoever.

Chapter 8 : Variable Selection

There are two main types of variable selection. The stepwise testing approach compares successive models while the criterion approach attempts to find the model that optimizes some measure of goodness.

The chapter starts off with discussing Hierarchical models. When selecting the variables it is important to respect the hierarchy. Lower order terms should not be removed before the higher order terms. Just pause for a minute here and think abt the reason? Why shouldn’t  Y = c + aX^2+ error be preferred over Y = c+ aX. I knew intuitively that it was incorrect to go with higher order terms with out the representation of lower order terms in the model. But never spent time on time on understanding the reason. The book explains it using a change of scale case where a model like Y = c + aX^2 becomes a model Y = c + bX + dX^2 with a simple change of scale. A change of scale in measuring a predictor variable should not change your linear model. That’s the reason why one must never consider higher order terms with out considering lower order terms. Thanks to this book, now I am able to verabalize the reason. As an aside, I got confused on reading the content under the heading “Hierarchical model”. Atleast to me, Hierarchical models are Bayesian in nature. Somehow the author seems to using this word loosely in this context. Or may it is ok to use this kind of terminology.

Three test based procedures are discussed for selecting variables, backward regression, forward regression and stepwise regression. The logic behind the procedures is obvious from their names. Backward regression means starting with all the predictors and removing one at a time based on their p values. Forward regression is starting with blank slate and incorporating the variable with least p value and continuing the process till there are no more variables to add. Stepwise is a mix of forward and backward. Even though these methods are easy to follow, the author cautions that these methods might not be completely reliable. The chapter asks the reader to keep the following points in mind :

1. Because of the “one-at-a-time” nature of adding/dropping variables, it is possible to miss the “optimal” model.

2. The p-values used should not be treated too literally. There is so much multiple testing occurring that the validity is dubious. The removal of less significant predictors tends to increase the significance of the remaining predictors. This effect leads one to overstate the importance of the remaining predictors.

3. The procedures are not directly linked to final objectives of prediction or explanation and so may not really help solve the problem of interest. With any variable selection method, it is important to keep in mind that model selection cannot be divorced from the underlying purpose of the investigation. Variable selection tends to amplify the statistical significance of the variables that stay in the model. Variables that are dropped can still be correlated with the response. It would be wrong to say that these variables are unrelated to the response; it is just that they provide no additional explanatory effect beyond those variables already included in the model.

4. Stepwise variable selection tends to pick models that are smaller than desirable for prediction purposes. To give a simple example, consider the simple regression with just one predictor variable. Suppose that the slope for this predictor is not quite statistically significant. We might not have enough evidence to say that it is related to y but it still might be better to use it for predictive purposes.

The last section in this chapter is titled , Criterion-based procedures. The basic funda behind these principle is as follows : You fit all possible models and select those models that fit a specific criterion, the criteria could be based on AIC or BIC or Mallow’s Cp or Adjusted R squared. I try to keep these four criteria in my working memory always. Why? I think I should atleast know a few basic stat measures to select models. Before thinking of fancy models, I want my working memory to be at least be on firm grounds as far as simple linear models are concerned.

The section kind of lays out a nice framework for going about simple linear modeling,i.e,

• Use regsubsets and get a list of models that fit the predictors and the dependent variable

• Compute Mallow’s cp for all the models, Adjusted R square for all the models

• Select a model based on the above criterion

• Use the four horse men of Linear Model Diagnostics (my own terminology just to remember things) and remove any unusual observations

• · Rerun the regsubsets again

As one can see, it is an iterative procedure, as it should be.

The author concludes the chapter by recommending criteria based selection methods over automatic selection methods.

**
Chapter 9 – Shrinkage Models**

The chapter is titled,”Shrinkage methods” for a specific reason, i.e. the methods used in this chapter help shrink the beta estimates in a linear regression framework. Typically in datasets where there are a large number of variables, modeling involves selecting the right variables and then regressing the optimal number of variables. How to decide the optional number of variables? If there are let’s say 100 variables, and you proceed by either backward/forward/step wise regression or criteria based regression, the parameters are going to be unstable. This chapter talks about three methods that can be used in the case of higher number of predicates. The underlying principle is the same, i.e. find some combination of predictor variables and reduce the dimension so that linear regression framework can be applied on this reduced space.

The first method mentioned in this chapter is PCA regression. You do a PCA on the data, select a few dimensions that capture the majority of variance, do a regression with those components. The idea here is dimension reduction coupled with a possible explanation of the PCA factors. Not always there is a good explanation of PCA factors. How to choose the number of factors ? Scree plot is the standard tool. However I learnt something new in this chapter, a cross validation principle based selection of the number of factors. There is a package called pls that has good functions to help a data analyst combine PCA based regression and cross validation principle

The second method mentioned in this chapter is Partial Least Squares, the essence of the method is to find various linear combinations of predictors and use that reduced dimension space to come up with a robust model. The problem with this kind of model is that you end up building a model with predictors that are extremely tough to explain to others. The chapter ends with the third method, ridge regression.

Chapter 10: Statistical Uncertainty and Model Uncertainty

This chapter talks about one of the most important aspects in data modeling, i.e model uncertainty. The previous chapter of the book covered three broad areas

• Diagnostics - Checking of assumptions-constant variance, linearity, normality , outliers, influential points , serial correlation and collinearity

• Transformations – Boxcox transformations, splines and polynomial regression

• Variable Selection – Testing and Criterion based methods

There is no hard and fast rule for following a specific sequence of steps. Sometimes diagnostics might be better first step, Sometimes Transformation could be a right step to begin with . I mean the order iin which the three steps , i.e Diagnostics, Transformations and Variable Selection needs to be followed is entirely dependent on the problem and the data analyst.

The author cites of an interesting situation , i.e asking his class of 28 students to estimate a linear model given the data. Obviously the author/professor knew the true model. By looking at each of 28 models submitted by his students he says that there was nothing inherently wrong in the way each of his student applied the above three steps. However the models that were submitted were vastly different from the true model. So were their root mean square errors and other model fit criteria.

The author cites this situation to highlight “Model Uncertainty” . Methods for realistic inference when the data are used to select the model have come to be known under “ Model Uncertainty”. The effects of model uncertainty often overshadow the parametric uncertainty and the standard errors need to be inflated to reflect this. This is one of the reasons why probably one should use different approaches to modeling and select those models that he / she feels confident about. It is very likely that a dozen modelers would come up with dozen different models. I guess for an individual data modeler, the best way is to approach the problem and frame it in various ways. May be use Bayesian modeling, use local regression framework, use MLE, etc. Build as many alternate models as possible and choose the predictors that concur amongst the majority, so it is more like Law of Large Models

I stumbled on an interesting paper by Freedman, titled “Some Issues in the Foundation of Statistics”, that talks about a common issue facing Bayesian and Frequentist modelers, i.e Model Validation. The paper is written extremely well and highlights the basic problem facing any modeler, “How to trust the model that one develops?”

Chapter 11 – Insurance Redlining – A case study

This case study touches on almost all the important concepts discussed in the previous 10 chapters. If a reader who wants to know whether it is worth reading this book, I guess the best way is to look at this dataset mentioned in this chapter, work for about 10-15 min on the data and check your analysis with the way author has gone about it. If you find the author’s way far more superior and elegant than yours, then it might be worth spending time on the book. In my case, the time and effort investment on this book has been pretty rewarding.

**
Chapter 12 Missing Data**

What do you do when there is missing data ? If the number of cases are small as compared to data, you can safely remove them from modeling. However if your dataset is small or is the missing data is crucial, then one needs to do missing treatment. This chapter talks about a few methods like mean fill in method and Regression fill in method. It also points to EM algo that is more sophisticated and applicable to practical problems. My perspective towards missing data treatment changed when I was told that there are PhDs employed in some hedge funds whose main job is to do missing treatment for security data. So, depending on your interest , curiosity and understanding levels, you can actually earn your living by doing missing data analysis!.

**
Chapter 13 - Analysis of Covariance**

This chapter talks about the case when there are qualitative predictors in the regression framework, basically the factor variables in R’s jargon. One can code the factor variable and use the same concepts, functions, packages that are discussed in the previous chapters. The chapter discusses two examples, the first example has predictor that takes only two levels and the second example has a predictor variable has more than 2 levels. The same combination of “Diagnostics-Transformation-Variable Selection” is used in a specific order to come up with a reasonable model.

**
Chapter 14 – One way Analysis of Variance**

ANOVA is the name referred to a linear modeling situation when the predictor is a factor variable with multiple levels. One can use the same linear model framework for this case too. One thing to remember is that when one is doing pair wise difference comparison, Tukeys Honest significant test is a better way to test than individual pair wise comparison tests.

The last two chapters of the book talk about factorial designs and block designs. Atleast I don’t see using the fundas from these chapters in my work. So, I have speed read them to get a basic overview of the principles involved.

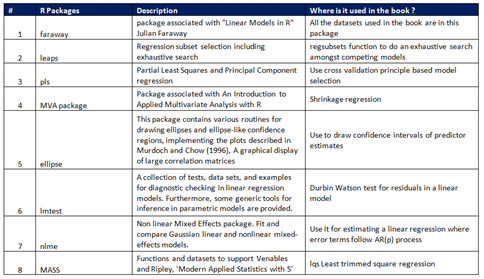
The good thing about this book is it comes with an R package that has all the datasets and several other functions used in the examples. Also the author makes use of about half a dozen packages. Have kept a track of the packages used by the author and here is the list of R packages used in the book :

[****Takeaway:

This book has one central focus through out all the chapters – Equip the reader to understand the nuts and bolts of regression modeling in R. The book explains in detail all aspects of linear modeling in R. Hence this book is highly appealing to someone who already knows the math behind linear models and wants to apply those principle to real life data using R.