Cashier Number 3 Please : Review

Reading this book was like revisiting an old services marketing course. This book is written by Terry Green, a guy who has been in to Queue management business for over 20 years. So, it is more a practitioner’s book written to help supermarket chains, banks, or any establishment that deals with customers who form a Queue to get serviced. This book does not have a single mathematical formula but intuitively covers many aspects of the math behind Queueing.
Let me mention briefly the kind of math that is used in analyzing Queues. A Queueing system is generally denoted by “A/B/X/Y/Z”, where A describes the arrival pattern for a system, B stands for the service pattern, X stands for the number of parallel service channels, Y the restriction of system capacity and Z , the queue discipline. If you want to analyze any system, you need to classify the system accordingly. Broadly the classification could be :
-
A – Arrivals can be Exponential, Deterministic, Erlang, Mixture of k exponentials, Phase type or Generic distribution
-
B – Servicing can be Exponential, Deterministic, Erlang, Mixture of k exponentials, Phase type or Generic distribution
-
X – # of parallel servers can be finite or infinite
-
Y – System capacity can be finite or infinite
-
Z – Queue discipline First come- First served , Last come – First Served , Random Selection for service, Priority Queue, General
Given these broad categories ,the number of queueing models can be as high as (6 arrival types*6 service types*2 types of servers *2 types of System capacity *5 types of Q discipline) as 720 different stochastic models. Add to this, customer behavior like Balking, Reneging, Jockeying, the number of models can actually explode. Well, the number 720 that I have mentioned here is an exaggeration. All queueing systems can be analyzed as a continuous time birth-death Markov process. If you understand let’s say G/G/1 queueing system, the rest of the systems are basically tweaks as far as problem formulation is concerned.The structure is more or less same but the way to solve the steady state equations differ. Generating functions/ Differential operators / Iterative methods/ Linear Algebra / Simulation are some of the various ways to find the steady state probabilities of the system. The more you assume exponential distribution for various components, the more your life become easy and most of the times you can derive closed form solutions. Beyond exponential arrival and exponential servicing, the math becomes fairly complicated.
I think that doing ONLY the math behind the queueing system creates a bias. Let me give an example.Imagine you are a graduate student and you are moonlighting at a cafeteria to earn some extra bucks. Let’s say , the inter arrivals of customers in to the cafeteria is an exponential distribution with average of 15 customers/ hr. The time you take to service each customer follows a Generic distribution , let’s say on an average you are able to serve a coffee in 3 minutes with a standard deviation of 1 minute. What’s the average Q size that might form in the cafeteria? Not to make things complicated, assume that the cafeteria has the capacity to accommodate infinite Queue length. Answering this simple question needs a fair amount of math (Pollaczek-Khintchine formula).But once one gets past the math and derives an expression, it is easy to think that everything is neat and water tight and that’s all there is to it. However even for this simple model, there are multiple real life aspects that need to be incorporated. Is it first of all M/G/1 queue ? Is there reneging or balking ? What if there are bulk arrivals(Usually a group of friends decide to have something and then head to the cafeteria). You can try to incorporate these things, but there are so many soft factors involved in the Queue formation that modeling the process and coming up with an implementable solution seems mind boggling. Extend this to supermarkets, hospitals, banks, call centers where there are multiple people servicing customer who do not behave as a standardized Poisson process or for that matter any stable generic distribution.
Books like these are valuable for two kinds of readers. First kind are those who believe that developing a right model is all that is there to Queue management. Second type are those who might not be using data/ statistics AT ALL to solve queueing problems in their service environments. This book is a bridge between the totally subjective way and totally scientific and objective way of handling queueing and service environments.
The author Terry Green is the founder of Qmatic system, a Queue management system that has been widely adopted in UK. Qmatic, has around 55,000 systems in 120 countries across the world. Roughly, a quarter of the world’s population benefit from fairer, faster service every year as a result. When the first installation of Qmatic was done, it so happened that, the cashier number 3 was available to be served for the customer waiting in the Q and hence the title of the book,”Cashier number 3 please”. Also the voice in Qmatic system is that of Terry Green.
The book starts off with emphasizing the perception of managing waiting times with an example from Disney theme parks.
Theme parks are about fun. People go there to experience the thrill of the attractions. And yet how much of the day is spent on the actual rides? Probably no more than 30%. The rest of the time is spent moving between rides, taking refreshment breaks, and queueing for the next ride. Theme parks have thus become the stars of the waiting game – and Disney indisputably the masters. Their work on managing the perception of waiting customers has been an integral part of the success of their parks.
Most of the businesses now care about the customer waiting times and try to systematically manage it. The author gives his first experience in Queue management at UK post offices
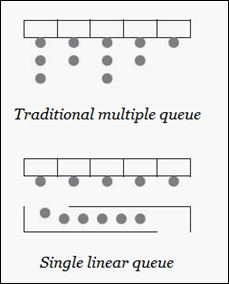
If you look at the above Queueing situations, the traditional multiple queue is still the one used in supermarkets and many other places. The book talks about the situation of Post offices in 1990 when the traditional multiple queue system was followed. Since there was no categorization of counters, some Qs moved very fast, some Qs took ages to move. Customers did all sorts of things like jockeying, balking, reneging etc. Obviously one had to come up with a better solution. Intuitively the Single linear queue is a better alternative as the effect of one guy taking a lot of time is not felt by others in the Q as they find other servers free.
One can prove that single linear queue is superior to traditional multiple queue by making a few assumptions( however some of the assumptions are questionable as we have noted in the cafeteria example). In the first case it is 5 independent M/M/1 systems.In the second case, the Queueing system is an M/M/5 system since there are 5 servers. The difference is that arrival rate for each server in the first system is 1/5th of the arrival rate of the second system. In fact it can be shown that any M/M/X system is better than X independent M/M/1 systems under certain assumptions(service rate is constant). One can easily show that the expected waiting time in the Q for traditional multiple Q is greater than Single linear Q.The math also concurs with our intuition that single linear queue system localizes the customers who have heavy server requirements.
After convincing the post office to convert single linear Q , there were subsequent problems to be solved. How does one tell the head of the Q member to proceed to the counter that is free. Since we are all used to Qing systems, we automatically think that there should be announcement and digital display for Queue management. However things did not evolve in such a straightforward manner. The author talks about various failed solutions before which the electronic counter + announcement made way to the post offices.
Around the same time, virtual Queueing was being adopted in European countries, where you book a place in the queue and then reach the server at the allotted time. There is a great debate on the question ,”Which Queueing system is better ?”. The author describes multiple cases where it is more a matter of convenience than anything else that differentiates between two systems. Even though the author starts off with analyzing the math and statistical aspects of Queueing systems, he realizes that managing perceptions of the customers was critical, i.e. behavioral models were far more important than statistical data models. The entire book contains a ton of cases where math aspects of Queueing had to combined with customer’s perception and customer’s expectation of the waiting time and service time.
You are certain to end up in a Queue somewhere or the other in your daily life, be it a supermarket store / bank / book store/ mall /waiting for a phone service rep. In all of these cases, the system is common. You have arrivals, you have queues and you have servers. This book at minimum will give you new eyes to look at a Queue. So, instead of getting frustrated in Queues and tiring yourself, you can quietly watch the queue dynamics and think about the things that are done well, the things that are being sidelined, the things that can be improved..After all, books you read, should make you curious about the world you live in and this book does a nice job of giving an intuitive reasoning for the Queueing systems that you encounter.