The Success Equation : Review

The title of the book gives away the main idea behind the book, i.e., ways to separate skill and luck in any outcome. Take any field, be it sports, investing, business , etc. all we get to see is the outcome. In games like chess, the outcome is clearly attributed to player’s “Skill” and in games like slot-machines / casino games, the outcome is clearly attributed to “Luck”. However there are a lot of activities that fall somewhere in between this Luck-Skill continuum. The book tries to answer the following questions :

How does one place an activity in the Luck-Skill continuum?
How does on quantify the components of Luck and Skill in any activity?
How do you account for changing / varying skills?
How does one improve the observed outcome for various activities on the Luck-Skill continuum?
What metrics does on use to capture the components of the outcome?
How does one verify whether the metrics are reliable or not?
What are the basic fallacies behind “mean reversion” ?
What is a better metric in the case where there is very little data to estimate?
What are the limitations of using quantitative methods for analysis of outcomes?
Why does great success always entail great luck?
How does the effect of sample size play in to the whole business of disentangling skill and luck ?
What are the kinds of models that one can think of, while analyzing “Luck”?
How does one get better in the art of good guesswork?
How to interpret feedback in luck dominated activity / skill dominated activity?

I will try to give a gist of the argument that the author makes throughout the book using a ton of examples , academic studies, and other books.

Think of the observed outcome as a random variable and assume the random variable is a linear combination of luck and skill. Simple model but it will do the job of getting the intuition right.

fig_1

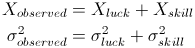
Think of 2 jars, the first one is a Luck jar and the second one is a Skill jar. Both jars contain marbles with different numbers on it. The proportion of a marbles with a specific number differs in both the jars. The simplest model one can think of is that the marbles in Luck jar and Skill jar are normally distributed with varying mean and standard deviation

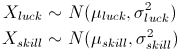
We get to see only the observables. So, in one sense inferring the distribution of skill and luck appears to be an intractable problem. The two distributions of luck and skill can take infinite forms and could result in the distribution that we get to see. So, how does one go about separating the skill and luck? To simplify thing further, one can assume the skill has less variance. Now things become a little easy to analyze. If there was no luck factor in the outcome, the following things would be evident in the observed data

Easily assign a cause to the effect / outcome.
Correlation between the outcomes is high.
There is slow rate of mean reversion.

The activities where such effects are visible are the ones where deliberate practice works, years of toiling at something makes you good at something. However if one sees that there is no correlation between outcomes, i.e. there is a faster mean reversion, then one can infer that Luck plays a great role in the outcome.

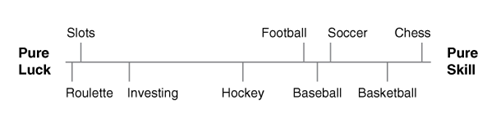
The sample size needed for the analysis of the outcomes depends on the type of activity. If it is a skill based activity, small sample size is ok. But in activities that are more toward the luck side, a big enough sample is a must. The basic problem with small sample sizes is that humans are extremely good at attaching a narrative to the data. A big sample size means that there is a possibility to see the luck component better.

Using the above two jar example the book suggests James Stein estimator for estimating true skill. The basic equation behind the estimator is

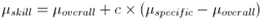
In the activities where there is huge amount of luck, the shrinkage factor c is close to 0 and in the activities that are more skill based one can use the shrinkage factor as 1. For the rest of the situations, one can estimate this shrinkage coefficient.

So, that’s the crux of the book. The author uses the above framework to various contexts such as baseball, investing, business strategies, etc. to show how one could analyze and apply the argument to various datasets. The book as such is well written and easy on eyes. Through various interesting examples, the author shows that one needs to always guesstimate the relative importance of skill and luck in various activities to avoid falling prey to various cognitive biases.

Here a list of random points in the book that I found interesting

The title of the author’s previous book “Think Twice” was crowd sourced. Mechanical Turk from Amazon was used to rate the various titles and “Think twice” came out as favorite
Feedback is largely misleading in activities where luck plays a significant part
“Can you lose on purpose” – is a simple test to check whether an activity is skill based or not ?
Analyzing “hot hands” involves checking whether a 2 state Markov model is statistically significant or not. I think the same analysis can be done on mutual funds to see whether there is a 2 or 3 state Markov chain model for the fund performance?
Polya’s urn framework to explain preferential treatment
Music Lab – The experiment run by Stanford prof to show that hits are actually difficult to predict. I found this experiment a powerful validation of how difficult it is to predict hits in the entertainment industry. Having said that, there is a mention of a bot in the the book “Automate this” that has predicted fair number of music hits. Which one to believe?
Correlation and rate of mean reversion capture the same effect
“Active share “ might be a good metric to analyze the performance of various funds.
When success is probabilistic, focus on the process
Fallacies of interpreting mean reversion – Illusion of cause and effect, Illusion of reduction in variance, Illusion of feedback.

Overall a thoroughly enjoyable read.