Parrondo’s Paradox : A combination of losing strategies becomes a winning strategy. 

This paradox can be seen via a simple simulation of three games.

  • Game Type 1 – You flip a biased coin that has 1/2-epsilon as the probability of heads. For each head you get $1 and for each tail you lose $1

  • Game Type 2 – If your capital is a multiple of 3, you flip a biased coin that has 1/10-epsilon, as probability of heads. If you capital is not a multiple of 3, you flip a biased coin that has 3/4-epsilon, as probability of heads . For each head you get $1 and for each tail you lose $1

  • Flip between Game Type 1 and Game Type 2 with equal probability – This is a combination of the two losing games. For each head you get $1 and for each tail you lose $1

If you just think about Game Type1, the fact that it is a losing proposition is a no brainer. Game Type 2 is also a losing game. You can either run a simulation or write a birth death chain for state transitions and verify that the state 0 is a recurrent state, i.e. game is a losing proposition.

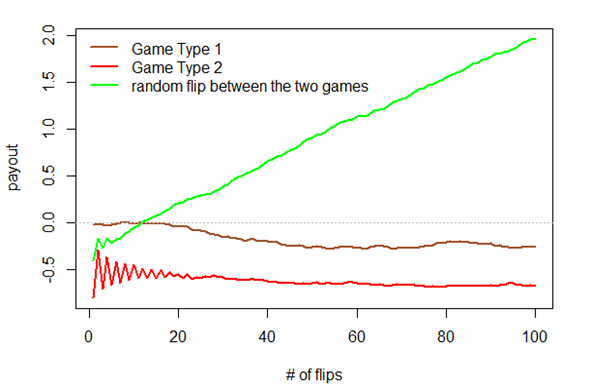
The following visual shows the average payoff for 100 flips for each of the above three games. I have taken epsilon as 1/1000 for the simulation. The paradox is that Game 3 has a positive payoff despite being a combination of games that have negative payoffs!

Parrando’s Paradox

What explains the paradox ? How can a combination of two losing games become a winning game ?

The resolution of the paradox comes from realizing that games are actually not independent. They are linked by the statement – “if the capital is a multiple of three, then …..”. Understanding this dependency is the key to resolving this paradox.