Biased vs. Unbiased

The following is a nice example from Michael Hardy that shows how excessive focus on unbiasedness of an estimator leads to nonsense results :

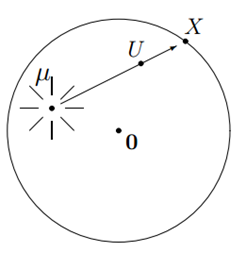
A light source is at an unknown location µ somewhere in the unit disk D. A dart thrown at the disk strikes some random location U in the disk, casting a shadow at a point X on the boundary. The random variable U is uniformly distributed in the disk, i.e., the probability that it is within any particular region is proportional to the area of the region. The boundary is a translucent screen, so that an observer located outside of the disk can see the location X of the shadow, but cannot see where either the light source or the opaque object is. Given only that information—the location X of the shadow—the location µ of the light source must be guessed. What’s your estimate of µ, given X ?

If you workout the unbiased frequentist estimate, it comes out as –2X, a totally absurd estimate of µ. On the other hand, a Bayesian estimate works out to be –X/4, a much more sensible and a reasonable estimate.