Purpose
To understand Uniform Convergence Page 183 - Bressound I

> epsilon <- 0.01
> par(mfrow = c(2, 2))
> x <- c(seq(-2, -9e-04, 1e-05), seq(9e-04, 2, 1e-05))
> n1 <- (epsilon/(3 * x * x - x * x * epsilon))
> plot(x, (n1), col = "blue")
> plot.new()
> x <- c(seq(-2, -0.21, 0.01), seq(0.21, 2, 0.01))
> n1 <- (epsilon/(3 * x * x - x * x * epsilon))
> n2 <- (3 - epsilon)/(epsilon * x * x)
> plot(x, (n1), col = "blue")
> plot(x, round(n2), col = "blue")

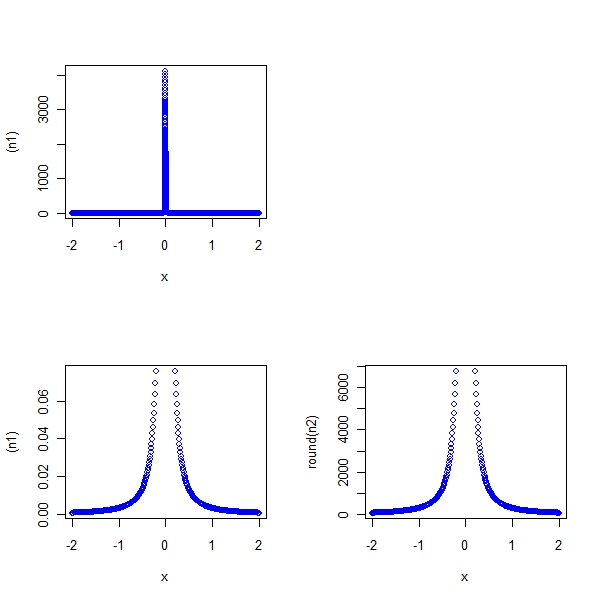
DP_March5_2010-001.jpg

As one can see , if you choose a specific small x so that size of first term
is less than epsilon/3, for the same x you have to choose a much much higher n it basically shoots to infinite.

Lets say at x = 0.1, you choose a specific n that satisfies second piece, that same n will never satisfy the first piece. Basically you cant win the epsilon delta game