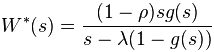Use of Continued Fractions for Laplace Transforms
In the case of a queueing model, it is very likely that service time distributions in a real life situation, do not have an exponential tail. This means that all the analytic solutions derived in any standard textbook are no longer applicable. If the server following a generic distribution, the expression linking the distributions such as Waiting time distribution, First passage time distributions, etc. and service time distributions is in the “Laplace Transform space”. This means that Laplace Transform of let’s say waiting time distribution is given as a function of Laplace transform of Service time distribution. For M/G/1, the waiting time distribution is given by the following expression :
In the above expression, g(s) denotes the Laplace transform of service time distributions. In all the situations where you can compute the value of g(s) at a given s , there are standard methods for numerical inversion. There are two methods described in this paper, one is Euler and second is Post-Widder method. Both can easily be implemented based on the code given the paper.
However the standard methods run in to difficulty when there is no explicit Laplace transform expressions for service time distribution. That’s where the ideas from the paper, “Computing Laplace Transforms for Numerical Inversion via Continued Fractions” are extremely useful.
In this post I will highlight the key ideas of the paper :
-
What’s the problem that the paper addresses ? There are situations where one does not have an explicit Laplace transform expression for service time distribution. How does on then, invert the Laplace transform ?
-
Where do such situations arise ? In all the cases where service time distributions have non-exponential tails
-
Continued fractions have a rich mathematical history. Continued fraction representation(cfe) serve as useful approximations for numbers. Like the way we have cfe for numbers, one can also have continued fraction representation to approximate a function.
-
The core idea of the paper is to represent the Laplace transform of service time distribution as a continued fraction, a special type of continued fraction, called the S fraction
-
There is a close connection between Laplace transform and coefficients of moment generating function. This is a trivial consequence of differentiating Laplace transform and observing that various moments of the distribution can be obtained. Hence Laplace transform can be written as a power series where coefficients are function of moments of the distribution
-
Power series can be approximated by Pade’ approximants, a tool for generating rational functions that approximate a power series
-
There is connection between Pade’ approximants of a power series and Continued fraction representation of a power series.
-
For completely monotone distribution functions, the Laplace transforms take a special continued fraction representation called S fractions
-
There is a very useful relationship between Laplace transform of a distribution function and the Laplace transform of its dual ccdf
The paper then uses the above ideas to show many situations where continued fractions can be applied. One of the examples is the first passage time distribution of a Birth-Death process. The Laplace transform of the first passage time distribution is written as a continued fraction by a recurrence relation. The elements of the continued fraction are obtained by diagonal elements in the Pade’ approximation matrix. Once the elements are obtained, the dual ccdf of first passage time can be obtained, from which first passage time distribution of the Birth-Death process can be obtained.
Some of the pre-requisites for understanding the paper are :
-
What is a continued fraction ? Where are they used ?
-
How can one use continued fraction to approximate a number or function ?
-
How does one compute the elements of a continued fraction ?
-
What are Pade approximants ? How are they computed ? How can they be used efficiently to approximate power series ?
-
When is a function completely monotone ? How do you characterize a completely monotone function ?
-
What are S fractions ?
-
Given any known Laplace transform of a function, how does one numerically invert it to obtain the original function ?
-
What are beta-mixture exponentials ? What are its variants ? What are ccdf and dual ccdf expressions for beta-mixture exponential distributions ?
-
What is a Gauss hypergeometric function ?
-
What is a Laguerre-series representation ?
It is definitely not a paper that can one can speed read. It has so many ideas and concepts that one might need multiple readings to fully understand it. The payoff from understanding the nuts and bolts of the paper is, one has a powerful numerical procedure in the toolbox to invert nasty Laplace transforms that one often comes across in real life modeling situations.